
【题目】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由.
(2)求∠DBE的度数.
(3)若把AD左右平行移动,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出此时∠ADB的度数;若不存在,请说明理由.

【答案】(1) AD∥BC,理由见解析;(2) 40°;(3)存在,∠ADB=60°
【解析】试题分析:(1)根据平行线的性质,以及等量代换证明∠ADC+∠C=180°,即可证得AD∥BC;(2)由直线AB∥CD,根据两直线平行,同旁内角互补,即可求得∠ABC的度数,又由∠DBE=![]() ∠ABC,即可求得∠DBE的度数.
∠ABC,即可求得∠DBE的度数.
(3)首先设∠ABD=∠DBF=∠BDC=x°,由直线AB∥CD,根据两直线平行,同旁内角互补与两直线平行,内错角相等,可求得∠BEC与∠ADB的度数,又由∠BEC=∠ADB,即可得方程:x°+40°=80°-x°,解此方程即可求得答案.
试题解析:(1)AD∥BC
理由:∵AB∥CD,
∴∠A+∠ADC=180°,
又∵∠A=∠C
∴∠ADC+∠C=180°,
∴AD∥BC;
(2)∵AB∥CD,
∴∠ABC=180°-∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE=![]() ∠ABF+
∠ABF+![]() ∠CBF=
∠CBF=![]() ∠ABC=40°;
∠ABC=40°;
(3)存在.
理由:设∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°-∠A=80°,
∴∠ADB=80°-x°.
若∠BEC=∠ADB,
则x°+40°=80°-x°,
得x°=20°.
∴存在∠BEC=∠ADB=60°.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知AB=2,C是AB上一点,四边形ACDE和四边形CBFG,都是正方形,设BC=x,
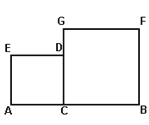
(1)AC=______;
(2)设正方形ACDE和四边形CBFG的总面积为S,用x表示S的函数解析式为S=_____.
(3)总面积S有最大值还是最小值?这个最大值或最小值是多少?
(4)总面积S取最大值或最小值时,点C在AB的什么位置?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.
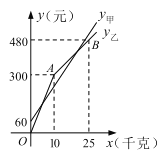
(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格;
![]()
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在将式子![]() (m>0)化简时,
(m>0)化简时,
小明的方法是:![]() =
=![]() =
=![]() =
=![]() ;
;
小亮的方法是: ![]() ;
;
小丽的方法是:![]() .
.
则下列说法正确的是( )
A. 小明、小亮的方法正确,小丽的方法不正确
B. 小明、小丽的方法正确,小亮的方法不正确
C. 小明、小亮、小丽的方法都正确
D. 小明、小丽、小亮的方法都不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A∶P′C=1∶3,则P′A∶PB=( )
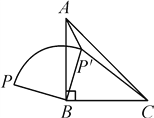
A. 1∶![]() B. 1∶2 C.
B. 1∶2 C. ![]() ∶2 D. 1∶
∶2 D. 1∶![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com