
【题目】已知AB=2,C是AB上一点,四边形ACDE和四边形CBFG,都是正方形,设BC=x,
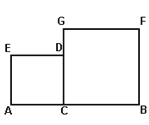
(1)AC=______;
(2)设正方形ACDE和四边形CBFG的总面积为S,用x表示S的函数解析式为S=_____.
(3)总面积S有最大值还是最小值?这个最大值或最小值是多少?
(4)总面积S取最大值或最小值时,点C在AB的什么位置?
【答案】(1)AC=2-x(0≤x≤2)(2)S=2![]() +2(3)4(4)当x=1时,C点恰好在AB的中点上;当x=0时,C点恰好在B处;当x=2时,C点恰好在A处
+2(3)4(4)当x=1时,C点恰好在AB的中点上;当x=0时,C点恰好在B处;当x=2时,C点恰好在A处
【解析】试题分析:(1)、根据AB=2得出AC的长度;(2)、根据总面积等于两个正方形的面积之和得出函数解析式;(3)、根据二次函数的增减性得出面积的最大值和最小值;(4)、根据最值时x的值得出AC的长度,从而得出点C的位置.
试题解析:(1)、当BC=x时,AC=2-x(0≤x≤2);
(2)、S△CDE=![]() ,S△BFG=
,S△BFG=![]() , 因此,S=
, 因此,S=![]() +
+![]() =2
=2![]() -4x+4=2
-4x+4=2![]() +2,
+2,
画出函数S=![]() +2(0≤x≤2)的图象如图:
+2(0≤x≤2)的图象如图:
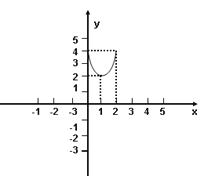
(3)、由图象可知:当x=1时, ![]() ;当x=0或x=2时,
;当x=0或x=2时, ![]() ;
;
(4)、当x=1时,C点恰好在AB的中点上;当x=0时,C点恰好在B处;当x=2时,C点恰好在A处.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】小明租用共享单车从家出发,匀速骑行到相距2400米的邮局办事.小明出发的同时,他的爸爸以每分钟100米的速度从邮局沿同一条道路步行回家,小明在邮局停留了2分钟后沿原路按原速返回.设他们出发后经过t(分)时,小明与家之间的距离为s1(米),小明爸爸与家之间的距离为s2(米),图中折线OABD,线段EF分别表示s1,s2与t之间的函数关系的图象.
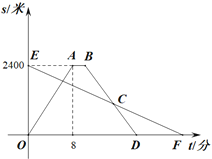
(1)求s1与t之间的函数表达式;
(2)小明从家出发,经过_______分在返回途中追上爸爸.
查看答案和解析>>
科目:初中数学 来源: 题型:
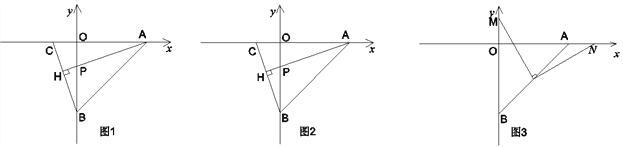
【题目】如图1,直线AB交x轴于点A(4 ,0),交y轴于点B(0 ,4),
(1)如图,若C的坐标为(-1, ,0),且AH⊥BC于点H,AH交OB于点P,试求点P的坐标;
(2)在(1)的条件下,如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连结MD,过点D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,式子![]() 的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
的值是否发生改变?如发生改变,求出该式子的值的变化范围;若不改变,求该式子的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知一次函数![]() (k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数
(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数![]() (m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.
(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D.若OA=OB=OD=1.

(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
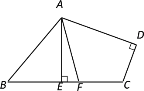
【题目】如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,学校准备购买一批课外读物,为使课外读物满足同学们的需求,学校就“我最喜爱的课外读物”从文学、艺术、科普和其他四个类别进行了抽样调查(每位同学只选一类),如图是根据调查结果绘制的两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学;
(2)条形统计图中,m,n的值;
(3)扇形统计图中,求出艺术类读物所在扇形的圆心角的度数;
(4)学校计划购买课外读物6000册,请根据样本数据,估计学校应购买其他类读物多少册?
查看答案和解析>>
科目:初中数学 来源: 题型:
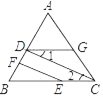
【题目】如图,已知EF⊥AB,CD⊥AB,下列说法:①EF∥CD;②∠B+∠BDG=180°;③若∠1=∠2,则∠1=∠BEF;④若∠ADG=∠B,则∠DGC+∠ACB=180°,其中说法正确的是( )
A. ①②B. ③④C. ①②③D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由.
(2)求∠DBE的度数.
(3)若把AD左右平行移动,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出此时∠ADB的度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
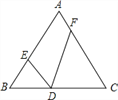
【题目】如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.
(1)求证:△BDE∽△CFD;
(2)当BD=1,CF=3时,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com