【题目】如图，
，
，
.给出下列结论：①
；②
；③
；④
.其中正确结论的序号是__________.
【答案】①②③
【解析】
根据三角形的内角和定理求出∠EAB=∠FAC，即可判断①；根据AAS证△EAB≌△FAC，即可判断②；推出AC=AB，根据ASA即可证出③；不能推出CD和DN所在的三角形全等，也不能用其它方法证出CD=DN．
∵∠E=∠F=90，∠B=∠C，
∵∠E+∠B+∠EAB=180，∠F+∠C+∠FAC=180，
∴∠EAB=∠FAC，
∴∠EABCAB=∠FAC∠CAB，
即∠1=∠2，∴①正确；
在△EAB和△FAC中
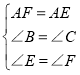
∴△EAB≌△FAC，
∴BE=CF，AC=AB，∴②正确；
在△ACN和△ABM中
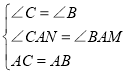
∴△ACN≌△ABM，∴③正确；
∵根据已知不能推出CD=DN，
∴④错误；
科目：初中数学 来源： 题型：
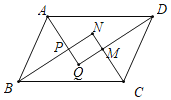
【题目】如图，在平行四边形ABCD中，AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线，AQ与BN相交于点P，CN与DQ相交于点M，判断四边形MNPQ的形状，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明租用共享单车从家出发，匀速骑行到相距2400米的邮局办事．小明出发的同时，他的爸爸以每分钟100米的速度从邮局沿同一条道路步行回家，小明在邮局停留了2分钟后沿原路按原速返回．设他们出发后经过t（分）时，小明与家之间的距离为s1（米），小明爸爸与家之间的距离为s2（米），图中折线OABD，线段EF分别表示s1，s2与t之间的函数关系的图象．
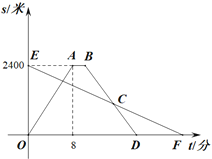
（1）求s1与t之间的函数表达式；
（2）小明从家出发，经过_______分在返回途中追上爸爸．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)请在横线上填写合适的内容，完成下面的证明：
如图①如果AB∥CD，求证：∠APC＝∠A+∠C．
证明：过P作PM∥AB．
所以∠A＝∠APM，( )
因为PM∥AB，AB∥CD(已知)
所以∠C＝ ( )
因为∠APC＝∠APM+∠CPM
所以∠APC＝∠A+∠C(等量代换)
(2)如图②，AB∥CD，根据上面的推理方法，直接写出∠A+∠P+∠Q+∠C＝ ．
(3)如图③，AB∥CD，若∠ABP＝x，∠BPQ＝y，∠PQC＝z，∠QCD＝m，则m＝ (用x、y、z表示)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD中AD∥BC, ∠B=60°，AB=AD=BO=4cm，OC=8cm, 点M从B点出发，按从B→A→D→C的方向，沿四边形BADC的边以1cm/s的速度作匀速运动，运动到点C即停止.若运动的时间为t，△MOD的面积为y,则y关于t的函数图象大约是( )
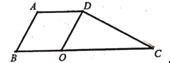
A.
B.
C.
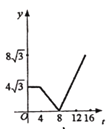D.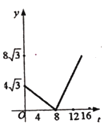
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（ ）
A. 函数有最小值
B. 对称轴是直线x=
C. 当x＜，y随x的增大而减小
D. 当﹣1＜x＜2时，y＞0
查看答案和解析>>
科目：初中数学 来源： 题型：
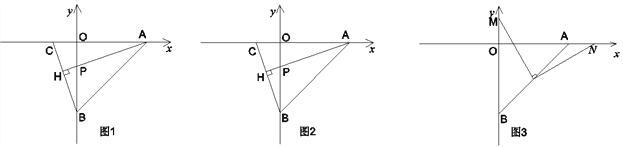
【题目】如图1，直线AB交x轴于点A（4 ，0），交y轴于点B（0 ，4），
（1）如图，若C的坐标为（-1, ，0），且AH⊥BC于点H，AH交OB于点P，试求点P的坐标；
（2）在（1）的条件下，如图2，连接OH，求证：∠OHP=45°；
（3）如图3，若点D为AB的中点，点M为y轴正半轴上一动点，连结MD，过点D作DN⊥DM交x轴于N点，当M点在y轴正半轴上运动的过程中，式子
的值是否发生改变？如发生改变，求出该式子的值的变化范围；若不改变，求该式子的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，已知一次函数
（k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数
（m≠0）的图象在第一象限交于C点，CD垂直于x轴，垂足为D．若OA=OB=OD=1．
（1）求点A、B、D的坐标；
（2）求一次函数和反比例函数的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线AB∥CD，∠A=∠C=100°，E、F在CD上，且满足∠DBF=∠ABD，BE平分∠CBF．
（1）直线AD与BC有何位置关系？请说明理由.
（2）求∠DBE的度数．
（3）若把AD左右平行移动，在平行移动AD的过程中，是否存在某种情况，使∠BEC=∠ADB？若存在，求出此时∠ADB的度数；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com