
【题目】如图,![]() 和
和![]() 是
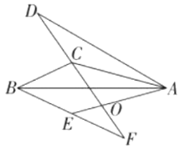
是![]() 分别沿着边AB、AC翻折180°形成的.DC的延长线交AE于点O,交BE的延长线于点F.若
分别沿着边AB、AC翻折180°形成的.DC的延长线交AE于点O,交BE的延长线于点F.若![]() ,,则
,,则![]() 的度数为_______.
的度数为_______.
【答案】30°
【解析】
根据∠BCA:∠ABC:∠BAC=28: 5: 3,三角形的内角和定理分别求得∠BCA,∠ABC,
∠BAC的度数,然后根据折叠的性质求出∠D、∠DAE、∠BEA的度数,在△AOD中,根据三角形的内角和定理求出∠AOD的度数,继而可求得∠EOF的度数,最后根据三角形的外角定理求出∠EFC的度数.
∵∠BCA:∠ABC:∠BAC=28:5:3,
∴设∠BCA为28x,∠ABC为5x,∠BAC为3x,
则28x+5x+3x=180°,
解得:x=5°,
则∠BCA=140°,∠ABC=25°,∠BAC=15°,
由折叠的性质可得:∠D=25°,∠DAE=3∠BAC=45°,∠BEA=140°,
在△AOD中,∠AOD=180°-∠DAE-∠D=110°,
∴∠EOF=∠AOD=110°,
∴∠EFC=∠BEA-∠EOF=140°-110°=30°.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】设实数a,b,c满足a>b>c(ac<0),且|c|<|b|<|a|,则|x-a|+|x+b|+|x-c|的最小值为( )
A. ![]() B. |b| C. a+b D. -c-a
B. |b| C. a+b D. -c-a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
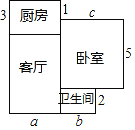
【题目】小王家新买的一套住房的建筑平面图如图所示(单位:米).
(1)这套住房的建筑总面积是多少平方米?(用含a,b,c的式子表示)
(2)若a=9,b=4,c=7,试求出小王家这套住房的具体面积.
(3)地面装修要铺设瓷砖,公司报价是:客厅地面每平方米200元,卧室地面每平方米150元,厨房地面每平方米120元,卫生间地面每平方米100元.在(2)的条件下,小王一共要花多少钱?
(4)这套住房的售价为每平方米4500元,购房时首付款为房价的40%,余款向银行申请贷款,在(2)的条件下,小宇家购买这套住房时向银行申请贷款的金额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
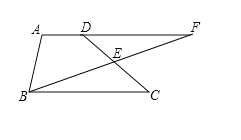
【题目】已知:如图,梯形ABCD中,AD∥BC,点E是CD的中点,BE的延长线与AD的延长线相交于点F.
(1)求证:△BCE≌△FDE.
(2)连接BD,CF,判断四边形BCFD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点与原点的距离相等.
(1)用“>”“<”或“=”填空:b______0,a+b______0,a-c______0,b-c______0;
(2)|b-1|+|a-1|=________;
(3)化简:|a+b|+|a-c|-|b|+|b-c|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连结DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y.
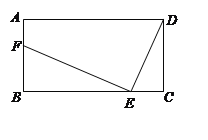
(1)求y关于x的函数关系式;
(2)若m=8,求x为何值时,y的值最大,最大值是多少?
(3)若![]() ,要使△DEF为等腰三角形,m的值应为多少?
,要使△DEF为等腰三角形,m的值应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】记:P1=﹣2,P2=(﹣2)×(﹣2),P3=(﹣2)×(﹣2)×(﹣2),…,![]() .
.
(1)计算P7÷P8的值;
(2)计算2P2019+P2020的值;
(3)猜想2Pn与Pn+1的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com