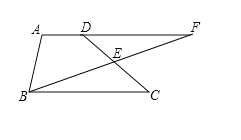
【题目】已知：如图，梯形ABCD中，AD∥BC，点E是CD的中点，BE的延长线与AD的延长线相交于点F．
（1）求证：△BCE≌△FDE．
（2）连接BD，CF，判断四边形BCFD的形状，并证明你的结论．
【答案】（1）见解析；（2）四边形BCFD是平行四边形，理由见解析
【解析】
（1）由平行线的性质可证，∠DFE=∠EBC，∠FDE=∠ECB，又已知DE=CE，在△BCE与△FDE中，根据三角形全等的判定定理，符合AAS的条件，即证△BCE≌△FDE．
（2）在1的基础上，可证DE=CE，FE=BE，根据平行四边形的判定，即证四边形BCFD是平行四边形．
证明：（1）∵点E是DC中点∴DE=CE
又∵AD∥BC，F在AD延长线上，∴∠DFE=∠EBC，∠FDE=∠ECB
在△BCE与△FDE中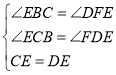
．
∴△BCE≌△FDE（AAS）
（2）四边形BCFD是平行四边形．理由如下：
∵△BCE≌△FDE，
∴DE=CE，FE=BE．
∴四边形BCFD是平行四边形．．
科目：初中数学 来源： 题型：
【题目】为提高中小学生的身体素质，各校大力开展校园足球活动，某体育用品商店抓住这一商机，第一次用30000元购进A、B两种型号的足球，并很快销售完，共获利12200元，其进价和售价如下表：
A | B | |
进价/（元/个） | 120 | 200 |
售价/（元/个） | 170 | 280 |
（1）体育用品商店购进A、B两种型号的足球各多少个？
（2）该体育用品商店第二次准备用不超过40000元的资金再次购进A、B两种型号的足球共260个，最少购进A种型号的足球多少个？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图（1），在Rt△ABC中，∠A=90°，AC=AB=4，D，E分别是AB，AC的中点．若等腰Rt△ADE绕点A逆时针旋转，得到等腰Rt△AD1E1，如图（2），设旋转角为α（0＜α≤180°），记直线BD1与CE1的交点为P．
（1）求证：BD1=CE1；（2）当∠CPD1=2∠CAD1时，求CE1的长；
（3）连接PA，△PAB面积的最大值为 ．（直接填写结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在某种特制的计算器中有一个按键
，它代表运算
．
例如：
上述操作即是求
的值，运算结果为1．
回答下面的问题：
（1）小敏的输入顺序为﹣6，
，﹣8，
，运算结果是 ；
（2）小杰的输入顺序为1，，-
，，，﹣2，
，-
，，
，3，，运算结果是 ；
（3）若在
这些数中，任意选取两个作为a、b的值，进行
运算，则所有的运算结果中最大的值是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
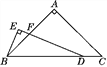
【题目】如图，△ABC中，AB＝AC，∠BAC＝90°，点D在线段BC上，∠EDB＝
∠C，BE⊥DE，垂足为E，DE与AB相交于点F.试探究线段BE与DF的数量关系，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，我们把对角线互相垂直的四边形叫做垂美四边形．
(l)概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由．
(2)性质探宄：试探索垂美四边形ABCD两组对边AB，CD与BC，AD之间的数量关系．
猜想结论:（要求用文字语言叙述）
写出证明过程（先画出图形，写出已知、求证）
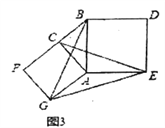
(3)问题解决：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接CE，BG，GE，已知AC=4，AB=5,求GE长．
查看答案和解析>>
科目：初中数学 来源： 题型：
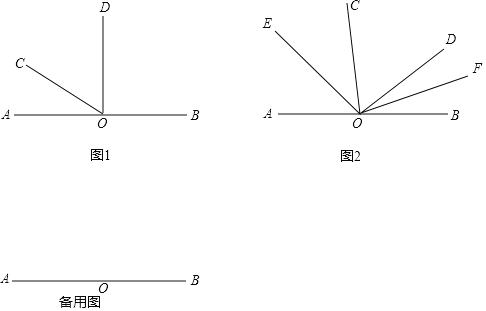
【题目】已知：如图1，点O是直线AB上的一点．
（1）如图1，当∠AOD是直角时，3∠AOC＝∠BOD，求∠COD的度数；
（2）若∠COD保持在（1）中的大小不变，它绕着点O顺时针旋转（OD与OB重合即停止），如图2，OE、OF分别平分∠AOC、∠BOD，则在旋转过程中∠EOF的大小是否变化？若不变，求出∠EOF的大小；若改变，说明理由；
（3）若∠COD从（1）中的位置开始，边OC、边OD分别绕着点O以每秒20°、每秒10°的速度顺时针旋转（当其中一边与OB重合时都停止旋转），OM、ON分别平分∠BOC、∠BOD．
求：①运动多少秒后，∠COD＝10°；
②运动多少秒后，∠COM＝∠BON．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
