
【题目】如图,在![]() 中,
中,![]() ,D、E点在AB上,
,D、E点在AB上,![]() ,
,![]() ,则
,则![]() 的大小是( )
的大小是( )

A.60°B.45°C.30°D.随![]() 的大小而变化
的大小而变化
科目:初中数学 来源: 题型:
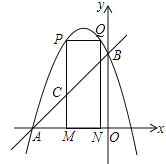
【题目】如图,直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P为抛物线在第二象限内一点,过点P作x轴的垂线,垂足为点M,与直线AB交于点C,过点P作x轴的平行线交抛物线于点Q,过点Q作x轴的垂线,垂足为点N,若点P在点Q左边,设点P的横坐标为m.
①当矩形PQNM的周长最大时,求△ACM的面积;
②在①的条件下,当矩形PMNQ的周长最大时,G是直线AC上一点,F是抛物线上一点,是否存在点G,使得以点P、C、G、F为顶点的四边形是平行四边形?若存在,请求出F点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点;又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是【A,B】的好点,但点D是【B,A】的好点.

知识运用:如图2,M、N为数轴上两点,点M所表示的数为-2,点N所表示的数为4.

(1)数______所表示的点是【M,N】的好点;
(2)如图3,A、B为数轴上两点,点A所表示的数为-20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法:
①这栋居民楼共有居民140人
②每周使用手机支付次数为28~35次的人数最多
③有![]() 的人每周使用手机支付的次数在35~42次
的人每周使用手机支付的次数在35~42次
④每周使用手机支付不超过21次的有15人
其中正确的是( )

A.①②B.②③C.③④D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
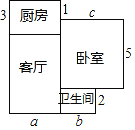
【题目】小王家新买的一套住房的建筑平面图如图所示(单位:米).
(1)这套住房的建筑总面积是多少平方米?(用含a,b,c的式子表示)
(2)若a=9,b=4,c=7,试求出小王家这套住房的具体面积.
(3)地面装修要铺设瓷砖,公司报价是:客厅地面每平方米200元,卧室地面每平方米150元,厨房地面每平方米120元,卫生间地面每平方米100元.在(2)的条件下,小王一共要花多少钱?
(4)这套住房的售价为每平方米4500元,购房时首付款为房价的40%,余款向银行申请贷款,在(2)的条件下,小宇家购买这套住房时向银行申请贷款的金额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
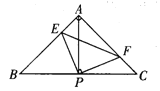
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,直角
,直角![]() 的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:①
的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:①![]() ;②
;②![]() 是等腰直角三角形;③
是等腰直角三角形;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的有( )
.其中正确的有( )
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
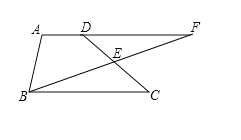
【题目】已知:如图,梯形ABCD中,AD∥BC,点E是CD的中点,BE的延长线与AD的延长线相交于点F.
(1)求证:△BCE≌△FDE.
(2)连接BD,CF,判断四边形BCFD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
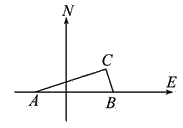
【题目】如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13nmile的A,B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120nmile,乙巡逻艇每小时航行50nmile,航向为北偏西40°,求甲巡逻艇的航向.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com