
ЁОЬтФПЁПШчЭМЃЌжБЯпy=x+3гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌХзЮяЯпy=Љx2+bx+cОЙ§AЁЂBСНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
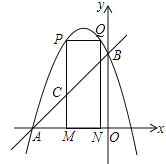
ЃЈ2ЃЉЕуPЮЊХзЮяЯпдкЕкЖўЯѓЯоФквЛЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌДЙзуЮЊЕуMЃЌгыжБЯпABНЛгкЕуCЃЌЙ§ЕуPзїxжсЕФЦНааЯпНЛХзЮяЯпгкЕуQЃЌЙ§ЕуQзїxжсЕФДЙЯпЃЌДЙзуЮЊЕуNЃЌШєЕуPдкЕуQзѓБпЃЌЩшЕуPЕФКсзјБъЮЊmЃЎ
ЂйЕБОиаЮPQNMЕФжмГЄзюДѓЪБЃЌЧѓЁїACMЕФУцЛ§ЃЛ
ЂкдкЂйЕФЬѕМўЯТЃЌЕБОиаЮPMNQЕФжмГЄзюДѓЪБЃЌGЪЧжБЯпACЩЯвЛЕуЃЌFЪЧХзЮяЯпЩЯвЛЕуЃЌЪЧЗёДцдкЕуGЃЌЪЙЕУвдЕуPЁЂCЁЂGЁЂFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіFЕуЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љx2Љ2x+3ЃЛЃЈ2ЃЉЂй![]() ЃЌЂкF1ЃЈЉ1ЃЌ4ЃЉЃЌF2ЃЈ
ЃЌЂкF1ЃЈЉ1ЃЌ4ЃЉЃЌF2ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌF3ЃЈ
ЃЉЃЌF3ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉЯШЧѓГіAЁЂBСНЕуЕФзјБъЃЌдйДњШыХзЮяЯпy=Љx2+bx+cЧѓГіbЁЂcЕФжЕМДПЩЃЛ
ЃЈ2ЃЉЂйЯШгУmБэЪОГіPMЕФГЄЃЌдйЧѓГіХзЮяЯпЕФЖдГЦжсМАPQЕФГЄЃЌРћгУОиаЮЕФУцЛ§ЙЋЪНПЩЕУГіЦфжмГЄЕФНтЮіЪНЃЌНјЖјПЩЕУГіОиаЮУцЛ§ЕФзюДѓжЕЃЌЧѓГіCЕузјБъЃЌгЩШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЕУГіНсТлЃЛ
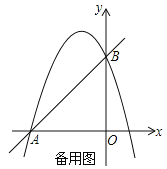
ЂкИљОнCЕузјБъЕУГіPЕузјБъЃЌЙЪПЩЕУГіPCЕФГЄЃЌдйЗжЕуFдкЕуGЕФЩЯЗНгыЕуFдкЕуGЕФЯТЗНСНжжЧщПіНјааЬжТлМДПЩЃЎ
ЯъНтЃКЃЈ1ЃЉЁпжБЯпy=x+3гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌЁрAЃЈЉ3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЎ
ЁпХзЮяЯпy=Љx2+bx+cОЙ§AЁЂBСНЕуЃЌЁр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љx2Љ2x+3ЃЛ
ЃЌЁрХзЮяЯпЕФНтЮіЪНЮЊy=Љx2Љ2x+3ЃЛ
ЃЈ2ЃЉЂйЁпЕуPЕФКсзјБъЮЊmЃЌЁрPЃЈmЃЌЉm2Љ2m+3ЃЉЃЌPM=Љm2Љ2m+3ЃЎ
ЁпХзЮяЯпy=Љx2Љ2x+3ЕФЖдГЦжсЮЊx=Љ![]() =Љ
=Љ![]() =Љ1ЃЌЁрPQ=2ЃЈЉ1ЉmЃЉ=Љ2mЉ2ЃЌЁрОиаЮPQMNЕФжмГЄ=2ЃЈPM+PQЃЉ=2ЃЈЉm2Љ2m+3Љ2mЉ2ЃЉ=Љ2m2Љ8m+2=Љ2ЃЈm+2ЃЉ2+10ЃЌЕБm=Љ2ЪБЃЌОиаЮPQMNЕФжмГЄзюДѓЃЌДЫЪБЕуCЕФзјБъЮЊЃЈЉ2ЃЌ1ЃЉЃЌCM=AM=1ЃЌЁрSЁїACM=
=Љ1ЃЌЁрPQ=2ЃЈЉ1ЉmЃЉ=Љ2mЉ2ЃЌЁрОиаЮPQMNЕФжмГЄ=2ЃЈPM+PQЃЉ=2ЃЈЉm2Љ2m+3Љ2mЉ2ЃЉ=Љ2m2Љ8m+2=Љ2ЃЈm+2ЃЉ2+10ЃЌЕБm=Љ2ЪБЃЌОиаЮPQMNЕФжмГЄзюДѓЃЌДЫЪБЕуCЕФзјБъЮЊЃЈЉ2ЃЌ1ЃЉЃЌCM=AM=1ЃЌЁрSЁїACM=![]() ЁС1ЁС1=
ЁС1ЁС1=![]() ЃЛ
ЃЛ
ЂкЁпCЃЈЉ2ЃЌ1ЃЉЃЌЁрPЃЈЉ2ЃЌ3ЃЉЃЌЁрPC=3Љ1=2ЃЎ
ЁпЕуPЁЂCЁЂGЁЂFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌGFЁЮyжсЃЌЁрGFЁЮ
ЩшGЃЈxЃЌx+3ЃЉЃЌдђFЃЈxЃЌЉx2Љ2x+3ЃЉЃЌЕБЕуFдкЕуGЕФЩЯЗНЪБЃЌЉx2Љ2x+3ЉЃЈx+3ЃЉ=2ЃЌНтЕУx=Љ1Лђx=Љ2ЃЈЩсШЅЃЉЃЌЕБx=Љ1ЪБЃЌЉx2Љ2x+3=4ЃЌМДF1ЃЈЉ1ЃЌ4ЃЉЃЛ
ЕБЕуFдкЕуGЕФЯТЗНЪБЃЌx+3ЉЃЈЉx2Љ2x+3ЃЉ=2ЃЌНтЕУЃКx=![]() Лђx=
Лђx=![]() ЃЎ
ЃЎ
ЕБx=![]() ЪБЃЌЉx2Љ2x+3=
ЪБЃЌЉx2Љ2x+3=![]() ЃЛ
ЃЛ
ЕБx=![]() ЪБЃЌЉx2Љ2x+3=
ЪБЃЌЉx2Љ2x+3=![]() ЃЌ
ЃЌ
ЙЪF2ЃЈ![]() ЃЉЃЌF3ЃЈ
ЃЉЃЌF3ЃЈ![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯЫљЪОЃЌЕуFЕФзјБъЮЊF1ЃЈЉ1ЃЌ4ЃЉЃЌF2ЃЈ![]() ЃЉЃЌF3ЃЈ
ЃЉЃЌF3ЃЈ![]() ЃЉЃЎ
ЃЉЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФЗНГЬx2Љkx+k2+nЃН0гаСНИіВЛЯрЕШЕФЪЕЪ§Иљx1ЁЂx2ЃЌЧвЃЈ2x1+x2ЃЉ2Љ8ЃЈ2x1+x2ЃЉ+15ЃН0ЃЎ
ЃЈ1ЃЉЧѓжЄЃКnЃМ0ЃЛ
ЃЈ2ЃЉЪдгУkЕФДњЪ§ЪНБэЪОx1ЃЛ
ЃЈ3ЃЉЕБnЃНЉ3ЪБЃЌЧѓkЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊAB//CDЃЌЕуCдкЕуDЕФгвВрЃЌЁЯABCЃЌЁЯADCЕФЦНЗжЯпНЛгкЕуE(ВЛгыBЃЌDЕужиКЯ).![]() ЃЌ
ЃЌ![]() .
.
(1)ШєЕуBдкЕуAЕФзѓВрЃЌЧѓЁЯBEDЕФЖШЪ§(гУКЌ![]() ЕФДњЪ§ЪНБэЪО).
ЕФДњЪ§ЪНБэЪО).
(2)НЋЯпЖЮBCбиDCЗНЯђЦНвЦЃЌЕБЕуBвЦЖЏЕНЕуAгвВрЪБЃЌЧыЛГіЭМаЮВЂХаЖЯ![]() ЕФЖШЪ§ЪЧЗёИФБф.ШєИФБфЃЌЧыЧѓГі
ЕФЖШЪ§ЪЧЗёИФБф.ШєИФБфЃЌЧыЧѓГі![]() ЕФЖШЪ§(гУКЌ
ЕФЖШЪ§(гУКЌ![]() ЕФДњЪ§ЪНБэЪО)ЃЛШєВЛБфЃЌЧыЫЕУїРэгЩ.
ЕФДњЪ§ЪНБэЪО)ЃЛШєВЛБфЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХЩчЛсЕФЗЂеЙЃЌЭЈЙ§ЮЂаХХѓгбШІЗЂВМздМКУПЬьаазпЕФВНЪ§вбОГЩЮЊвЛжжЪБЩаЃЎЁАНЁЩэДяШЫЁБаЁГТЮЊСЫСЫНтЫћЕФКУгбЕФдЫЖЏЧщПіЃЎЫцЛњГщШЁСЫВПЗжКУгбНјааЕїВщЃЌАбЫћУЧ6дТ1ШеФЧЬьаазпЕФЧщПіЗжЮЊЫФИіРрБ№ЃКAЃЈ0ЁЋ5000ВНЃЉЃЈЫЕУїЃКЁА0ЁЋ5000ЁББэЪОДѓгкЕШгк0ЃЌаЁгкЕШгк5000ЃЌЯТЭЌЃЉЃЌBЃЈ5001ЁЋ10000ВНЃЉЃЌCЃЈ10001ЁЋ15000ВНЃЉЃЌDЃЈ15000ВНвдЩЯЃЉЃЌЭГМЦНсЙћШчЭМЫљЪОЃК

ЧывРОнЭГМЦНсЙћЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮЕїВщжаЃЌвЛЙВЕїВщСЫЁЁ ЁЁЮЛКУгбЃЎ
ЃЈ2ЃЉвбжЊAРрКУгбШЫЪ§ЪЧDРрКУгбШЫЪ§ЕФ5БЖЃЎ
ЂйЧыВЙШЋЬѕаЮЭМЃЛ
ЂкЩШаЮЭМжаЃЌЁАAЁБЖдгІЩШаЮЕФдВаФНЧЮЊЁЁ ЁЁЖШЃЎ
ЂлШєаЁГТЮЂаХХѓгбШІЙВгаКУгб150ШЫЃЌЧыИљОнЕїВщЪ§ОнЙРМЦДѓдМгаЖрЩйЮЛКУгб6дТ1ШеетЬьаазпЕФВНЪ§ГЌЙ§10000ВНЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЙ§ЕуAЃЈ2ЃЌ0ЃЉЕФСНЬѕжБЯп![]() ЃЌ
ЃЌ![]() ЗжБ№НЛ
ЗжБ№НЛ![]() жсгкBЃЌCЃЌЦфжаЕуBдкдЕуЩЯЗНЃЌЕуCдкдЕуЯТЗНЃЌвбжЊAB=
жсгкBЃЌCЃЌЦфжаЕуBдкдЕуЩЯЗНЃЌЕуCдкдЕуЯТЗНЃЌвбжЊAB=![]() .
.

ЃЈ1ЃЉЧѓЕуBЕФзјБъЃЛ
ЃЈ2ЃЉШєЁїABCЕФУцЛ§ЮЊ4ЃЌЧѓ![]() ЕФНтЮіЪНЃЎ
ЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌвбжЊжБЯпABЕФКЏЪ§НтЮіЪНЮЊy=Љ2x+8ЃЌгыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉШєЕуPЃЈmЃЌnЃЉЮЊЯпЖЮABЩЯЕФвЛИіЖЏЕуЃЈгыAЁЂBВЛжиКЯЃЉЃЌзїPEЁЭxжсгкЕуEЃЌPFЁЭyжсгкЕуFЃЌСЌНгEFЃЌЮЪЃК
ЂйШєЁїPAOЕФУцЛ§ЮЊSЃЌЧѓSЙигкmЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіmЕФШЁжЕЗЖЮЇЃЛ
ЂкЪЧЗёДцдкЕуPЃЌЪЙEFЕФжЕзюаЁЃПШєДцдкЃЌЧѓГіEFЕФзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЬсИпжааЁбЇЩњЕФЩэЬхЫижЪЃЌИїаЃДѓСІПЊеЙаЃдАзуЧђЛюЖЏЃЌФГЬхг§гУЦЗЩЬЕъзЅзЁетвЛЩЬЛњЃЌЕквЛДЮгУ30000дЊЙКНјAЁЂBСНжжаЭКХЕФзуЧђЃЌВЂКмПьЯњЪлЭъЃЌЙВЛёРћ12200дЊЃЌЦфНјМлКЭЪлМлШчЯТБэЃК
A | B | |
НјМл/ЃЈдЊ/ИіЃЉ | 120 | 200 |
ЪлМл/ЃЈдЊ/ИіЃЉ | 170 | 280 |
ЃЈ1ЃЉЬхг§гУЦЗЩЬЕъЙКНјAЁЂBСНжжаЭКХЕФзуЧђИїЖрЩйИіЃП
ЃЈ2ЃЉИУЬхг§гУЦЗЩЬЕъЕкЖўДЮзМБИгУВЛГЌЙ§40000дЊЕФзЪН№дйДЮЙКНјAЁЂBСНжжаЭКХЕФзуЧђЙВ260ИіЃЌзюЩйЙКНјAжжаЭКХЕФзуЧђЖрЩйИіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаМзЁЂввСНжжПЭГЕЃЌ2СОМзжжПЭГЕгы3СОввжжПЭГЕЕФзмдиПЭСПЮЊ180ШЫЃЌ1СОМзжжПЭГЕгы2СОввжжПЭГЕЕФзмдиПЭСПЮЊ105ШЫЃЎ
ЃЈ1ЃЉЧыЮЪ1СОМзжжПЭГЕгы1СОввжжПЭГЕЕФдиПЭСПЗжБ№ЮЊЖрЩйШЫЃП
ЃЈ2ЃЉФГбЇаЃзщжЏ240УћЪІЩњМЏЬхЭтГіЛюЖЏЃЌФтзтгУМзЁЂввСНжжПЭГЕЙВ6СОЃЌвЛДЮНЋШЋВПЪІЩњЫЭЕНжИЖЈЕиЕуЃЎШєУПСОМзжжПЭГЕЕФзтН№ЮЊ400дЊЃЌУПСОввжжПЭГЕЕФзтН№ЮЊ280дЊЃЌЧыИјГізюНкЪЁЗбгУЕФзтГЕЗНАИЃЌВЂЧѓГізюЕЭЗбгУЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌDЁЂEЕудкABЩЯЃЌ
ЃЌDЁЂEЕудкABЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФДѓаЁЪЧЃЈ ЃЉ
ЕФДѓаЁЪЧЃЈ ЃЉ

A.60ЁуB.45ЁуC.30ЁуD.Ыц![]() ЕФДѓаЁЖјБфЛЏ
ЕФДѓаЁЖјБфЛЏ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com