
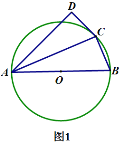
【题目】如图1,![]() 是
是![]() 的外接,
的外接,![]() 是直径,
是直径,![]() 是
是![]() 外一点且满足
外一点且满足![]() ,连接
,连接![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,
,![]() ,求直径
,求直径![]() 的长;
的长;
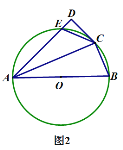
(3)如图2,当![]() 时,
时,![]() 与
与![]() 交于
交于![]() 点,试写出
点,试写出![]() 、
、![]() 、
、![]() 之间的数量关系并证明.
之间的数量关系并证明.
【答案】(1)见详解;(2)5;(3)![]() ,证明见详解
,证明见详解
【解析】
(1)连接OC,由OB=OC知∠OCB=∠B,结合∠DCA=∠B得∠DCA=∠OCB,再由AB是直径知∠ACB=90°,据此可得∠DCA+∠ACO=∠OCB+∠ACO=90°,从而得证;
(2)先利用勾股定理求得AC=2![]() ,再证△ADC∽△ACB得
,再证△ADC∽△ACB得![]() ,据此求解可得;
,据此求解可得;
(3)连接BE,在AC上截取AF=BC,连接EF..由AB是直径、∠DAB=45°知∠AEB=90°,据此得△AEB是等腰直角三角形,AE=BE,再证△ECB≌△EFA得EF=EC,据此可知△FEC是等腰直角三角形,从而得出![]() ,从而得证.
,从而得证.
解:(1)证明:连接OC.
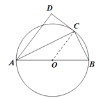
∵OB=OC
∴∠OCB=∠B
∵∠DCA=∠B
∴∠DCA=∠OCB
∵AB是直径
∴∠ACB=90
∴∠DCA+∠ACO =∠OCB+∠ACO=90,
即∠DCO=90,
∴CD是⊙O的切线
(2)∵AD⊥CD,CD=2,AD=4.
∴![]() ,
,
由(1)可知∠DCA=∠B,∠D=∠ACB=90
∴△ADC∽△ACB
∴![]()
∴![]()
∴AB=5.
(3)![]() ,
,
如图2,连接BE,在AC上截取AF=BC,连接EF.

∵AB是直径,∠DAB=45
∴∠AEB=90
∴△AEB是等腰Rt△
∴AE=BE
又∵∠EAC=∠EBC,
∴△ECB≌△EFA
∴EF=EC,∵∠ACE=∠ABE=45
∴△FEC是等腰Rt△
∴![]()
∴![]() .
.


科目:初中数学 来源: 题型:
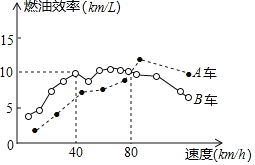
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油最多可行驶的公里数,如图描述了A、B两辆汽车在不同速度下的燃油效率情况.
根据图中信息,下面4个推断中,合理的是( )
①消耗1升汽油,A车最多可行驶5千米;
②B车以40千米/小时的速度行驶1小时,最多消耗4升汽油;
③对于A车而言,行驶速度越快越省油;
④某城市机动车最高限速80千米/小时,相同条件下,在该市驾驶B车比驾驶A车更省油.
A.①④B.②③C.②④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形 ABCD 中,E 为 BC 边中点.
(Ⅰ)已知:如图,若 AE 平分∠BAD,∠AED=90°,点 F 为 AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD

(Ⅱ)已知:如图,若 AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点 F,G 均为 AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+ ![]() BC+CD.
BC+CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x。

(1)求证:△PFA∽△ABE;
(2)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
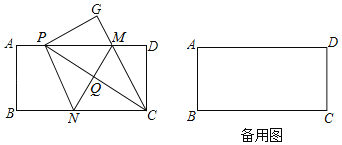
【题目】如图,现有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN丁点Q,连接CM.
(1)求证:PM=PN;
(2)当P,A重合时,求MN的值;
(3)若△PQM的面积为S,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC的边AB,AC的外侧分别作等边△ABD和等边△ACE,连接DC,BE.
(1)求证:DC=BE;
(2)若BD=3,BC=4, BD⊥BC于点B,请求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
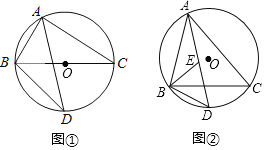
【题目】已知△ABC是⊙O的内接三角形,∠BAC的平分线交⊙O于点D.
(I)如图①,若BC是⊙O的直径,BC=4,求BD的长;
(Ⅱ)如图②,若∠ABC的平分线交AD于点E,求证:DE=DB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙只捕捞船同时从A港出海捕鱼,甲船以每小时15![]() km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
(1)甲船从C处出发追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com