
【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数![]() 与方差s2如下表所示:
与方差s2如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲B. 乙C. 丙D. 丁
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在一个口袋中有4个完全相同的小球,把它们分别标号1、2、3、4.小明先随机地摸出一个小球,小强再随机地摸出一个小球.记小明摸出球的标号为x,小强摸出的球标号为y.小明和小强在此基础上共同协商一个游戏规则:当x>y时小明获胜。否则小强获胜.
(1)若小明摸出的球不放回,求小明获胜的概率;
(2)若小明摸出的球放回后小强再随机摸球,问他们制定的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2、4、6、8,…排成如下表,并用一个十字形框架住其中的五个数,请你仔细观察十字形框架中数字的规律,并回答下列问题:
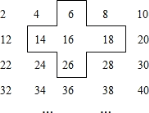
![]() 十字框中的五个数的和与中间的数16有什么关系?
十字框中的五个数的和与中间的数16有什么关系?
![]() 设中间的数为x,用代数式表示十字框中的五个数的和.
设中间的数为x,用代数式表示十字框中的五个数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…+22019的值.
解:设S=1+2+22+23+24+…+22018+22019,①将等式两边同时乘2,得
2S=2+22+23+24+25+…+22019+22020,②
将②式减去①式,得2S-S=22020-1,
即S=22020-1,
则1+2+22+23+24+…+22019=22020-1.
请你仿照此法计算:
(1)1+2+22+23+24+…+210;
(2)1+3+32+33+34+…+3n(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题:
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为a1,依次类推,排在第n位的数称为第n项,记为an.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母q表示(q≠0).如:数列1,3,9,27,…为等比数列,其中a1=1,公比为q=3.
则:(1)等比数列3,6,12,…的公比q为 ,第4项是 .
(2)如果一个数列a1,a2,a3,a3,…是等比数列,且公比为q,那么根据定义可得到:
![]() ,……
,…… ![]() .
.
∴a2=a1q,a3=a2q=(a1q)q=a1q2,a4=a3q=(a1q2)q= a1q3,……
由此可得:an= (用a1和q的代数式表示)
(3)若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=-2x与直线l2:y=kx+b在同一平面直角坐标系内交于点P .
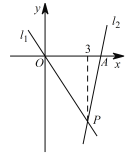
(1)直接写出不等式-2x>kx+b 的解集 ;
(2)设直线l2 与x 轴交于点A ,△OAP的面积为12 ,求l2的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
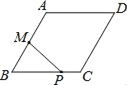
A. 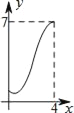 B.
B. 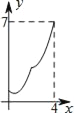 C.
C. 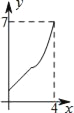 D.
D. 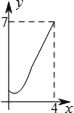
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
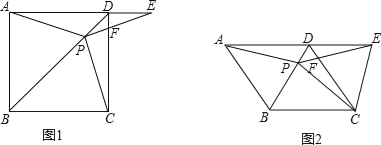
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com