
【题目】看图填空,并在括号内说明理由: 如图,已知∠BAP与∠APD互补,∠1=∠2,说明∠E=∠F.
∵∠BAP与∠APD互补,
∴∠E=∠F. . 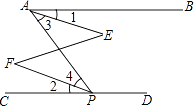
【答案】已知;同旁内角互补,两直线平行;两直线平行,内错角相等;已知;等量代换;内错角相等,两直线平行;两直线平行,内错角相等
【解析】证明:∵∠BAP与∠APD互补(已知), ∴AB∥CD(同旁内角互补,两直线平行),
∴∠BAP=∠APC( 两直线平行,内错角相等).
又∵∠1=∠2(已知),
∴∠BAP﹣∠1=∠APC﹣∠2(等量代换),即∠3=∠4,
∴AE∥PF,(内错角相等,两直线平行),
∴∠E=∠F( 两直线平行,内错角相等).
所以答案是:已知;同旁内角互补,两直线平行;两直线平行,内错角相等;已知;等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
【考点精析】本题主要考查了余角和补角的特征和平行线的判定与性质的相关知识点,需要掌握互余、互补是指两个角的数量关系,与两个角的位置无关;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数. 小明的解题思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图3,AD∥BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.试判断∠CPD、∠α、∠β之间有何数量关系? 请说明理由;
(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)![]() = ,
= , ![]() = ,
= , ![]() = ,
= , ![]() = ,
= , ![]() = ,
= ,
(2)根据计算结果,回答: ![]() 一定等于a吗?你发现其中的规律了吗?请你把得到规律描述出来.
一定等于a吗?你发现其中的规律了吗?请你把得到规律描述出来.
(3)利用你总结的规律,计算: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图: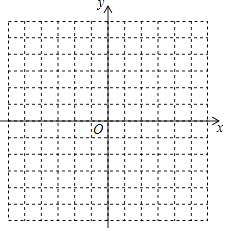
(1)在如图所示的平面直角坐标系中表示下面各点:
A(0,3);B(5,0);C(3,﹣5);D(﹣3,﹣5);E(3,5);
(2)A点到原点的距离是?
(3)将点C向x轴的负方向平移6个单位,它与哪个点重合.
(4)连接CE,则直线CE与y轴是什么位置关系?
(5)点D分别到x、y轴的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学生为调查本校学生平均每天完成作业所用时间的情况,随机调查了50名同学,下图是根据调查所得数据绘制的统计图的一部分.
请根据以上信息,解答下列问题:
(1)将统计图补充完整;
(2)若该校共有1800名学生,根据以上调查结果估计该校全体学生每天完成作业所用总时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法).
(2)直接写出A′、B′、C′三点的坐标:
A′(); B′();
C′( ).
(3)求△ABC的面积 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍.设调往甲处植树x人,则可列方程( )
A.23﹣x=2(17+20﹣x)B.23﹣x=2(17+20+x)
C.23+x=2(17+20﹣x)D.23+x=2(17+20+x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),  BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com