
����Ŀ�������龳����ͼ1��AB��CD����PAB=130�㣬��PCD=120�㣮���APC������ С���Ľ���˼·�ǣ���ͼ2����P��PE��AB��ͨ��ƽ�������ʣ��ɵá�APC=50��+60��=110�㣮
����Ǩ�ƣ�
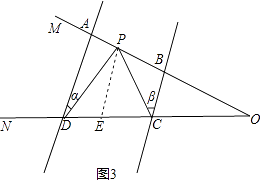
��1����ͼ3��AD��BC����P������OM���˶�������P��A��B����֮���˶�ʱ����ADP=�Ϧ�����BCP=�Ϧ£����жϡ�CPD���Ϧ����Ϧ�֮���к�������ϵ�� ��˵�����ɣ�
��2���ڣ�1���������£������P��A��B��������˶�ʱ����P���A��B��O���㲻�غϣ�������ֱ��д����CPD���Ϧ����Ϧ¼��������ϵ��
���𰸡�
��1���⣺��CPD=�Ϧ�+�Ϧ£��������£�
��ͼ3����P��PE��AD��CD��E��
��AD��BC��
��AD��PE��BC��
��Ϧ�=��DPE���Ϧ�=��CPE��
���CPD=��DPE+��CPE=�Ϧ�+�Ϧ£�
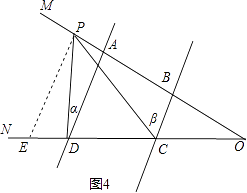
��2���⣺��P��BA�ӳ���ʱ����CPD=�Ϧ©��Ϧ���
���ɣ���ͼ4����P��PE��AD��CD��E��
��AD��BC��
��AD��PE��BC��
��Ϧ�=��DPE���Ϧ�=��CPE��
���CPD=��CPE����DPE=�Ϧ©��Ϧ���
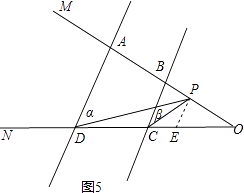
��P��AB�ӳ���ʱ����CPD=�Ϧ����Ϧ£�
���ɣ���ͼ5����P��PE��AD��CD��E��
��AD��BC��
��AD��PE��BC��
��Ϧ�=��DPE���Ϧ�=��CPE��
���CPD=��DPE����CPE=�Ϧ����Ϧ£�
����������1����P��PE��AD��CD��E���Ƴ�AD��PE��BC������ƽ���ߵ����ʵó��Ϧ�=��DPE���Ϧ�=��CPE�����ɵó��𰸣���2������ͼ�Σ�������������ٵ�P��BA���ӳ����ϣ��ڵ�P��AB���ӳ����ϣ�������ƽ���ߵ����ʵó��Ϧ�=��DPE���Ϧ�=��CPE�����ɵó��𰸣�
�����㾫��������ƽ���ߵ������ǽ����ĸ�������Ҫ֪����ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У��ڴ�����ȣ���ֱ��ƽ�У�ͬ���ڽǻ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
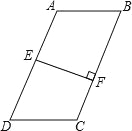
����Ŀ����ͼ�����ı���ABCD�У�AB��DC��E��AD�е㣬EF��BC�ڵ�F��BC=5��EF=3��
��1����AB=DC�����ı���ABCD�����S= ��
��2����AB��DC�����ʱ�ı���ABCD�����S�� S���á�������=����������գ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�� ![]() ��
�� ![]() ��
�� ![]() ����ͼ��ʽ���У����涨��m��n����ʾ��m�Ŵ������ҵ�n��������6��5���루13��6����ʾ������֮���ǣ�������
����ͼ��ʽ���У����涨��m��n����ʾ��m�Ŵ������ҵ�n��������6��5���루13��6����ʾ������֮���ǣ������� 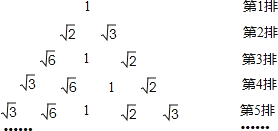
A.![]()
B.6
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
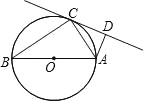
����Ŀ����ͼ��AB�ǡ�O��ֱ����C�ǡ�O��һ�㣬��ACD=��B��AD��CD��
��1����֤��CD�ǡ�O�����ߣ�
��2����AD=1��OA=2����AC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ 3a3 bn �� 5am+1 b4���õĺ����ǵ���ʽ���� m n ��ֵΪ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ�������·��������40������ڶ����ȹ��������162�������ó��塢���·�ƽ��ÿ�µ�������Ϊx����ôx����ķ����ǣ�������
A.40��1+x��2=162
B.40+40��1+x��+40��1+x��2=162
C.40��1+2x��=162
D.40+40��1+x��+40��1+2x��=162
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��أ���������ǵĶ���_____����ô���Ǿ�˵����������ȣ���������ǵĶ���______����ô���Ǿ�˵�����ϴ�Ľǽϴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��գ�����������˵�����ɣ� ��ͼ����֪��BAP���APD��������1=��2��˵����E=��F��
�ߡ�BAP���APD������
���E=��F�� �� 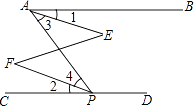
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com