
 ��ͼ�����κ���y=ax2+bx+c��ͼ����x���ཻ�ڵ�A��-3��0���͵�B����y�ύ�ڵ�C������D������Ϊ��-1��4������P�ǵڶ��������������ϵ�һ���㣬����P��PM��x����M�����߶�AC�ڵ�E��
��ͼ�����κ���y=ax2+bx+c��ͼ����x���ཻ�ڵ�A��-3��0���͵�B����y�ύ�ڵ�C������D������Ϊ��-1��4������P�ǵڶ��������������ϵ�һ���㣬����P��PM��x����M�����߶�AC�ڵ�E������ ��1������ϵ�����ɷֱ���ö��κ�����һ�κ�������ʽ��
��2����PH��y�ᣬ����PC�����P��a��-a2-2a+3������ʾ��PH��OH��AO��CH�ij�����S��PAC=S����PHOA-S��PCH-S��AOC=3�ó�����a�ķ��̣���⼴�ɵ�a��ֵ������֪��P�����ꣻ
��3������P��m��-m2-2m+3��������PQMN���ܳ�ΪC�����ݾ����ܳ���ʽ��ʾ��C����m�ĺ�������ʽ���������ֵ�������֪��P���꣬���ֱ��AC�Ľ���ʽ���ɵ�֪EM�ij���
�ڸ��ݢ�֪��P��E��C���꣬���PE��PC��CE�ij������жϡ�PCE����״��
��� �⣺��1����������������߽���ʽΪy=a��x+1��2+4��
����A��-3��0�����룬�ã�4a+4=0��
��ã�a=-1��
�������߽���ʽΪy=-��x+1��2+4=-x2-2x+3��
���C������0��3����
��ֱ��AC�Ľ���ʽΪy=kx+b��
����A��-3��0����C��0��3�����룬�ã�$\left\{\begin{array}{l}{-3k+b=0}\\{b=3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪy=x+3��
��2����ͼ����PH��y�ᣬ����PC��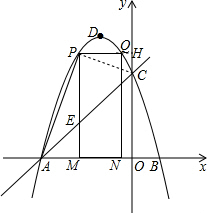
���P��a��-a2-2a+3����
��PH=-a��OH=-a2-2a+3��OA=3��
��S��PAC=S����PHOA-S��PCH-S��AOC=3��
��$\frac{1}{2}$����-a+3����-a2-2a+3��-$\frac{1}{2}$����-a����-a2-2a+3-3��-$\frac{1}{2}$��3��3=3��
�������ã�a2+3a+2=0��
��ã�a=-1��a=-2��
���P��������-1��4����-2��3����
��3������P��m��-m2-2m+3��������PQMN���ܳ�ΪC��
��PQ=-2m-2��PM=-m2-2m+3��
��C=2[��-2m-2��+��-m2-2m+3��]
=-2m2-8m+2
=-2��m+2��2+10��
�൱m=-2ʱ������PQMN���ܳ����ʱ��P��-2��3����
��x=-2ʱ��y=x+3=-2+3=1����EM=1��
���ɢ�֪��E��-2��1����
�ߵ�P��-2��3����C��0��3����
��PE=2��PC=2��CE=$\sqrt{��-2-0��^{2}+��1-3��^{2}}$=2$\sqrt{2}$��
��PE2+PC2=CE2����PE=PC��
���PCE�ǵ���ֱ�������Σ�
���� ���⿼���˶��κ�������ʽ�����ʣ����ε����ʡ�һԪ���η��̵Ľⷨ��֪ʶ���ۺ��Խ�ǿ���������ν�ϡ�����˼���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����������β�ȱ��һ���֣�A��B��C��������ε�3�����㣬��������εĶ���B��ֱ��l��AC������1=36�㣬��������εı���Ϊ��������
��ͼ��ʾ����������β�ȱ��һ���֣�A��B��C��������ε�3�����㣬��������εĶ���B��ֱ��l��AC������1=36�㣬��������εı���Ϊ��������| A�� | 4 | B�� | 5 | C�� | 6 | D�� | 7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ��������ABCD������ƽ��ֱ������ϵ�У�����AB����y���ϣ���C����Ϊ��4��0����ֱ��m��$y=-\frac{4}{3}x-3$������B������ֱ������y����ÿ��1����λ���ٶ�����ƽ�ƣ���ƽ��ʱ��Ϊt��������Dʱֹͣƽ�ƣ�
��ͼ��ʾ��������ABCD������ƽ��ֱ������ϵ�У�����AB����y���ϣ���C����Ϊ��4��0����ֱ��m��$y=-\frac{4}{3}x-3$������B������ֱ������y����ÿ��1����λ���ٶ�����ƽ�ƣ���ƽ��ʱ��Ϊt��������Dʱֹͣƽ�ƣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��x | ��x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| ��y | ��1 | 3�� | 7 | 13 | 21 | 31 | 43 |
| x�� | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
| y | y1 | y2 | y3 | y4 | y5 | y6 | y7 |
| ��x | ��x1 | x2 | x3 | x4 | x5 | ��x6 | x7 |
| ��y | ��10 | 50�� | ��110 | 190�� | 290�� | 412�� | ��550 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڱ߳�Ϊ6��������ABCD�У���������ABCD�Ƶ�A��ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������AEFG��EF���߶�CD�ڵ�P��FE���ӳ��߽��߶�BC�ڵ�H������AH��AP��
��ͼ���ڱ߳�Ϊ6��������ABCD�У���������ABCD�Ƶ�A��ʱ����ת�ǶȦ���0�㣼����90�㣩���õ�������AEFG��EF���߶�CD�ڵ�P��FE���ӳ��߽��߶�BC�ڵ�H������AH��AP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��̽���о������ǿ��Խ����ǰ�о������ľ��飬̽������y=x+$\frac{1}{x}$��x��0����ͼ�����ʣ�
��̽���о������ǿ��Խ����ǰ�о������ľ��飬̽������y=x+$\frac{1}{x}$��x��0����ͼ�����ʣ�| X | �� | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | �� |
| y | �� | $\frac{17}{4}$ | $\frac{10}{3}$ | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | $\frac{17}{4}$ | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��һ�κ���y=k2x+b��ͼ����y�ύ�ڵ�B��������������y=k1x��ͼ���ཻ�ڵ�A��4��3������OA=OB��
��ͼ��һ�κ���y=k2x+b��ͼ����y�ύ�ڵ�B��������������y=k1x��ͼ���ཻ�ڵ�A��4��3������OA=OB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com