
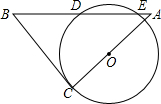
 如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )| A. | 3cm | B. | $\frac{20}{7}$cm | C. | $\sqrt{10}$cm | D. | 2$\sqrt{2}$cm |
科目:初中数学 来源: 题型:解答题
| 课题 | 测量教学楼高度 | |
| 方案 | 方案一 | 方案二 |
| 测量示意图 | 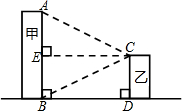 |  |
| 测得数据 | BD=32m,∠ACE=∠BCE=31° | BD=32m,∠DAF=50°,∠CAF=31° |
| 参考数据 | tan31°≈0.60,sin31°≈0.52 cos31°≈0.86 | tan31°≈0.60,tan50°≈1.20, sin50°≈0.77 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
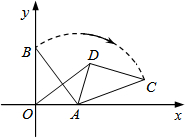 在平面直角坐标系中,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD.当∠DOA=∠OBA时,直线CD的解析式为y=-$\frac{7}{24}$x+4.
在平面直角坐标系中,已知点A(3,0),B(0,4),将△BOA绕点A按顺时针方向旋转得△CDA,连接OD.当∠DOA=∠OBA时,直线CD的解析式为y=-$\frac{7}{24}$x+4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
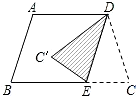 如图,在梯形ABCD中,AD∥BC,AB=DC,∠ABC=72°,现平行移动腰AB至DE后,再将△DCE沿DE折叠,得△DC′E,则∠EDC′的度数是( )
如图,在梯形ABCD中,AD∥BC,AB=DC,∠ABC=72°,现平行移动腰AB至DE后,再将△DCE沿DE折叠,得△DC′E,则∠EDC′的度数是( )| A. | 72° | B. | 54° | C. | 36° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
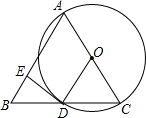 如图,已知△ABC,AB=AC,以边AC为直径作⊙O,BC与圆交于点D,过D作DE⊥AB于E.
如图,已知△ABC,AB=AC,以边AC为直径作⊙O,BC与圆交于点D,过D作DE⊥AB于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com