
| 课题 | 测量教学楼高度 | |
| 方案 | 方案一 | 方案二 |
| 测量示意图 | 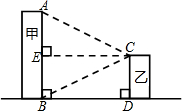 |  |
| 测得数据 | BD=32m,∠ACE=∠BCE=31° | BD=32m,∠DAF=50°,∠CAF=31° |
| 参考数据 | tan31°≈0.60,sin31°≈0.52 cos31°≈0.86 | tan31°≈0.60,tan50°≈1.20, sin50°≈0.77 |
分析 方案一:首先四边形BDCE是矩形,则可得CE=BD=32cm,CD=BE,然后分别在Rt△ACE与Rt△BCE中,利用三角函数的知识,求得AE与BE的长,继而求得答案;
方案二:首先连接AD,易得四边形BDCE是矩形,则可得CE=BD=32cm,CD=BE,然后分别在Rt△ACE与Rt△ABD中,利用三角函数的知识,求得AE与BE的长,继而求得答案
解答 解:方案一:根据题意得:四边形BDCE是矩形,
∴CE=BD=32cm,CD=BE,
在Rt△ACE中,AE=EC•tan31°≈32×0.60=19.20(m),
在Rt△BCE中,BE=EC•tan31°≈32×0.60=19.20(m),
∴AB=AE+BE=38.40m,CD=BE=19.20m;
答:甲教学楼AB的高度为:38.40m;乙教学楼CD的高度为19.20m;
方案二:如图,连接AD,
根据题意得:四边形BDCE是矩形,
∴CE=BD=32cm,CD=BE,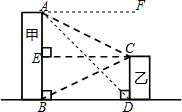
∵在Rt△ACE中,∠ACE=∠CAF=31°,
∴AE=EC•tan31°≈32×0.60=19.20(m),
∵在Rt△ABD中,∠ADB=∠DAF=50°,
∴AB=BD•tan50°≈32×1.20=38.40(m),
∴CD=BE=AB-AE=19.20m.
答:甲教学楼AB的高度为:38.40m;乙教学楼CD的高度为19.20m.
点评 本题考查仰角与俯角的定义.注意能借助仰角与俯角构造直角三角形并解直角三角形是关键.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为( )
如图,小“鱼”与大“鱼”是位似图形,已知小“鱼”上一个“顶点”的坐标为(a,b),那么大“鱼”上对应“顶点”的坐标为( )| A. | (-a,-2b) | B. | (-2a,-b) | C. | (-2a,-2b) | D. | (-b,-2a) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<b | B. | c>-1 | C. | a>-3 | D. | c<-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -1 | 3 | 5 | 3 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
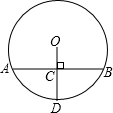 如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )
如图,已知⊙O的半径OD与弦AB互相垂直,垂足为点C,若AB=16cm,CD=6cm,则⊙O的半径为( )| A. | $\frac{25}{3}$cm | B. | 10cm | C. | 8cm | D. | $\frac{19}{3}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
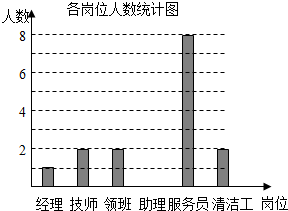 某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表
某公司共20名员工,员工基本工资的平均数为2200元.现就其各岗位每人的基本工资情况和各岗位人数,绘制了下列尚不完整的统计图表:各岗位每人的基本工资情况统计表| 岗位 | 经理 | 技师 | 领班 | 助理 | 服务员 | 清洁工 |
| 基本工资 | 10000 | 4000 | 2400 | 1600 | 1000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
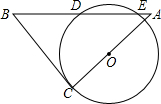 如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )
如图,将一块等腰Rt△ABC的直角顶点C放在⊙O上,绕点C旋转三角形,使边AC经过圆心O,某一时刻,斜边AB在⊙O上截得的线段DE=2cm,且BC=7cm,则OC的长为( )| A. | 3cm | B. | $\frac{20}{7}$cm | C. | $\sqrt{10}$cm | D. | 2$\sqrt{2}$cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com