
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -1 | 3 | 5 | 3 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据表格数据求出二次函数的对称轴为直线x=1.5,然后根据二次函数的性质对各小题分析判断即可得解.
解答 解:(1)由图表中数据可得出:x=1时,y=5,所以二次函数y=ax2+bx+c开口向下,a<0;又x=0时,y=3,所以c=3>0,所以ac<0,故(1)正确;
(2)∵二次函数y=ax2+bx+c开口向下,且对称轴为x=1.5,∴当x≥1.5时,y的值随x值的增大而减小,故(2)错误;
(3)∵x=3时,y=3,∴9a+3b+c=3,∵c=3,∴9a+3b+3=3,∴9a+3b=0,∴3是方程ax2+(b-1)x+c=0的一个根,故(3)正确;
(4)∵x=-1时,ax2+bx+c=-1,∴x=-1时,ax2+(b-1)x+c=0,∵x=3时,ax2+(b-1)x+c=0,且函数有最大值,∴当-1<x<3时,ax2+(b-1)x+c>0,故(4)正确.
故选C.
点评 本题考查了二次函数的性质,二次函数图象与系数的关系,抛物线与x轴的交点,二次函数与不等式,有一定难度.熟练掌握二次函数图象的性质是解题的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 课题 | 测量教学楼高度 | |
| 方案 | 方案一 | 方案二 |
| 测量示意图 | 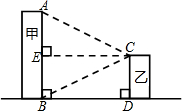 |  |
| 测得数据 | BD=32m,∠ACE=∠BCE=31° | BD=32m,∠DAF=50°,∠CAF=31° |
| 参考数据 | tan31°≈0.60,sin31°≈0.52 cos31°≈0.86 | tan31°≈0.60,tan50°≈1.20, sin50°≈0.77 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
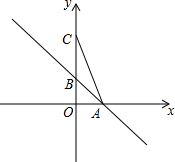 如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B.点C在y轴的正半轴上,且sin∠ACB=$\frac{\sqrt{10}}{10}$
如图,一次函数y=-x+1的图象与x轴、y轴分别交于点A、B.点C在y轴的正半轴上,且sin∠ACB=$\frac{\sqrt{10}}{10}$ 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
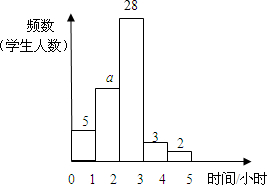 某中学九年级(1)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
某中学九年级(1)班50名学生参加平均每周上网时间的调查,由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
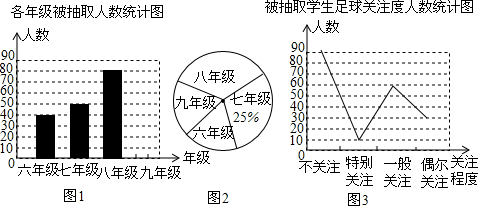
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com