
【题目】如图,在△ABC中,∠C=90°,AB的垂直平分线DE交AC于D,垂足为E,若∠A=30°,CD=3.
(1)求∠BDC的度数.
(2)求AC的长度.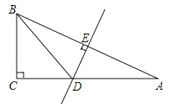
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2017的坐标为( )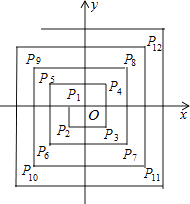
A.(504,﹣504)
B.(﹣504,504)
C.(﹣504,503)
D.(﹣505,504)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电商场将一款电视机按进价提高40%定价,再写上“八折酬宾”,结果每台电视机盈利不低于240元,则电视机的进价至少为每台________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式(17x2﹣3x+4)﹣(ax2+bx+c)能被5x整除,且商式为2x+1,则a﹣b+c=( )
A. 12 B. 13 C. 14 D. 19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB, 改变△ACD的位置(其中A点位置始终不变),使三角形ACD的一边与三角形AOB的某一边平行时,写出∠BAD的所有可能的值 . 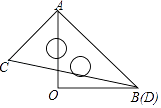
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com