练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．已知一元二次方程2x2-5x+3=0，则该方程根的情况是（　　）
    A．有两个不相等的实数根B．有两个相等的实数根
    C．两个根都是自然数D．无实数根

    分析 判断上述方程的根的情况，只要看根的判别式△=b2-4ac的值的符号就可以了．

    解答 解：∵a=2，b=-5，c=3，
    ∴△=b2-4ac=（-5）2-4×2×3=1＞0，
    ∴方程有两个不相等的实数根．
    故选：A．

    点评 此题主要考查了一元二次方程根的判别式，掌握一元二次方程根的情况与判别式△的关系：（1）△＞0?方程有两个不相等的实数根；（2）△=0?方程有两个相等的实数根；（3）△＜0?方程没有实数根，是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．如图，在△ABC中，AB=AC，AD是边BC上的高，求证：
    （1）BD=DC；
    （2）∠BAD=∠CAD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连结BD、DP，BD与CF相交于点H．给出下列结论：
    ①△ABE≌△DCF；②$\frac{FP}{PH}$=$\frac{3}{5}$；③DP2=PH•PB；④$\frac{{S}_{△BPD}}{{S}_{正方形ABCD}}$=$\frac{\sqrt{3}-1}{4}$．
    其中正确的是①③④．（写出所有正确结论的序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

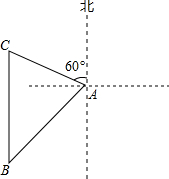    11．如图，海中一小岛上有一个观测点A，某天上午9：00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行．当天上午9：30观测到该渔船在观测点A的北偏西60°方向上的C处．若该渔船的速度为每小时30海里，在此航行过程中，问该渔船从B处开始航行多少小时，离观测点A的距离最近？（计算结果用根号表示，不取近似值）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．宁波火车站北广场将于2015年底投入使用，计划在广场内种植A，B两种花木共6600棵，若A花木数量是B花木数量的2倍少600棵
    （1）A，B两种花木的数量分别是多少棵？
    （2）如果园林处安排26人同时种植这两种花木，每人每天能种植A花木60棵或B花木40棵，应分别安排多少人种植A花木和B花木，才能确保同时完成各自的任务？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．从-2，-1，0，1，2这5个数中，随机抽取一个数记为a，则使关于x的不等式组$\left\{\begin{array}{l}{\frac{2x-1}{6}≥-\frac{1}{2}}\\{2x-1＜2a}\end{array}\right.$有解，且使关于x的一元一次方程$\frac{3x-a}{2}$+1=$\frac{2x+a}{3}$的解为负数的概率为$\frac{3}{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．某小组7位学生的中考体育测试成绩（满分30分）依次为27，30，29，27，30，28，30．则这组数据的众数与中位数分别是（　　）
    A．30，27B．30，29C．29，30D．30，28

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．方程$\frac{{x}^{2}+x}{x+1}$=0的解是x=0；方程y2+9=6y的解是y1=y2=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．b2m•b4n-2m=b4n；（am）2=a2m．

    查看答案和解析>>

    同步练习册答案