
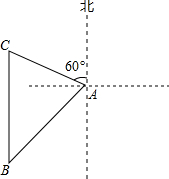
 如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).
如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值). 分析 首先根据题意可得PC⊥AB,然后设PC=x海里,分别在Rt△APC中与Rt△APB中,利用正切函数求得出PC与BP的长,由PC+BP=BC=30×$\frac{1}{2}$,即可得方程,解此方程求得x的值,再计算出BP,然后根据时间=路程÷速度即可求解.
解答  解:过点A作AP⊥BC,垂足为P,设AP=x海里.
解:过点A作AP⊥BC,垂足为P,设AP=x海里.
在Rt△APC中,∵∠APC=90°,∠PAC=30°,
∴tan∠PAC=$\frac{CP}{AP}$,
∴CP=AP•tan∠PAC=$\frac{\sqrt{3}}{3}$x.
在Rt△APB中,∵∠APB=90°,∠PAB=45°,
∴BP=AP=x.
∵PC+BP=BC=30×$\frac{1}{2}$,
∴$\frac{\sqrt{3}}{3}$x+x=15,
解得x=$\frac{15(3-\sqrt{3})}{2}$,
∴PB=x=$\frac{15(3-\sqrt{3})}{2}$,
∴航行时间:$\frac{15(3-\sqrt{3})}{2}$÷30=$\frac{3-\sqrt{3}}{4}$(小时).
答:该渔船从B处开始航行$\frac{3-\sqrt{3}}{4}$小时,离观测点A的距离最近.
点评 此题考查了解直角三角形的应用-方向角问题,锐角三角函数的定义,准确作出辅助线构造直角三角形是解题的关键,注意数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
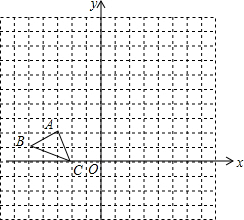 在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-3,2),B(-5,1),C(-2,0),点P(a,b)是△ABC的AC边上的一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+5,b+2).
在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-3,2),B(-5,1),C(-2,0),点P(a,b)是△ABC的AC边上的一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+5,b+2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
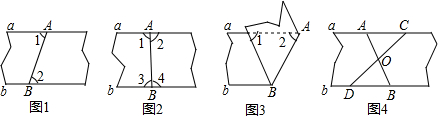
| A. | 如图1,展开后测得∠1=∠2 | |
| B. | 如图2,展开后测得∠1=∠2且∠3=∠4 | |
| C. | 如图3,测得∠1=∠2 | |
| D. | 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 两个根都是自然数 | D. | 无实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com