
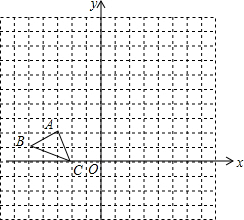
 在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-3,2),B(-5,1),C(-2,0),点P(a,b)是△ABC的AC边上的一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+5,b+2).
在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-3,2),B(-5,1),C(-2,0),点P(a,b)是△ABC的AC边上的一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+5,b+2).分析 (1)根据P点对应点变化规律得出△ABC平移规律进而求出即可;
(2)借助网格利用勾股定理逆定理得出△ABC的形状.
解答 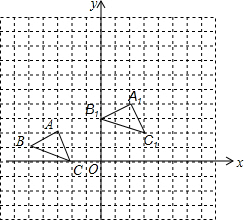 解:(1)∵点P(a,b)是△ABC的AC边上的一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+5,b+2),
解:(1)∵点P(a,b)是△ABC的AC边上的一点,△ABC经过平移后得到△A1B1C1,点P的对应点为P1(a+5,b+2),
∴A(-3,2),B(-5,1),C(-2,0)的对应点坐标分别为:A1(2,4),B1(0,3),C1(3,2),
如图所示:△A1B1C1,即为所求;
(2)如图所示:AB=$\sqrt{5}$,AC=$\sqrt{5}$,则BC=$\sqrt{10}$,
故AB2+AC2=BC2,
则△ABC是等腰直角三角形.
点评 此题主要考查了勾股定理逆定理以及图形的平移,根据题意得出平移规律是解题关键.


科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}2x-3≤3\\ \frac{1}{2}x+1>0\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}2x-3≤3\\ \frac{1}{2}x+1>0\end{array}\right.$,并把解集在数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
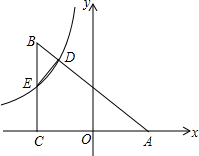 如图,△ABC顶点A在x轴上,∠BCA=90°,AC=4,BC=3,反比例函数y=-$\frac{4}{3x}$(x<0)的图象分别与AB,BC交于点D,E.设点E、D的横坐标分别为a、b,连结DE,当△BDE∽△BCA时,a、b的关系式为b=$\frac{1}{a}$.
如图,△ABC顶点A在x轴上,∠BCA=90°,AC=4,BC=3,反比例函数y=-$\frac{4}{3x}$(x<0)的图象分别与AB,BC交于点D,E.设点E、D的横坐标分别为a、b,连结DE,当△BDE∽△BCA时,a、b的关系式为b=$\frac{1}{a}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 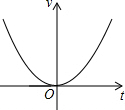 | B. |  | C. | 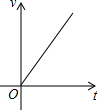 | D. | 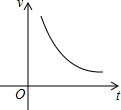 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
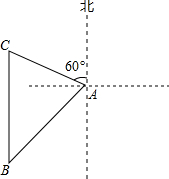 如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).
如图,海中一小岛上有一个观测点A,某天上午9:00观测到某渔船在观测点A的西南方向上的B处跟踪鱼群由南向北匀速航行.当天上午9:30观测到该渔船在观测点A的北偏西60°方向上的C处.若该渔船的速度为每小时30海里,在此航行过程中,问该渔船从B处开始航行多少小时,离观测点A的距离最近?(计算结果用根号表示,不取近似值).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com