
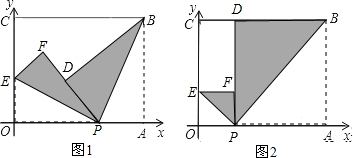
分析 (1)根据题目条件得出Rt△POE∽Rt△BPA,然后根据相似三角形的性质列出比例式,转化为关于x的二次函数最值问题解答;
(2)设出二次函数的一般式,利用待定系数法列出方程组,求出a、b、c的值即可得到经过E、P、B三点的抛物线的解析式.
解答 解:(1)由已知PB平分∠APD,PE平分∠OPF,且PD、PF重合,则∠BPE=90°,
∴∠OPE+∠APB=90°.
又∵∠APB+∠ABP=90°,
∴∠OPE=∠PBA,
∴Rt△POE∽Rt△BPA,
∴$\frac{PO}{OE}$=$\frac{BA}{AP}$.即$\frac{x}{y}$=$\frac{2}{3-x}$,
∴y=$\frac{1}{2}$x(3-x)=-$\frac{1}{2}$x2+$\frac{3}{2}$x=-$\frac{1}{2}$(x-$\frac{3}{2}$)2+$\frac{9}{8}$(0<x<3),
∴当x=$\frac{3}{2}$时,y有最大值$\frac{9}{8}$;
(2)由已知得,△PAB、△POE均为等腰三角形,
则P(1,0),E(0,1),B(3,2).
设过此三点的抛物线为y=ax2+bx+C,
则$\left\{\begin{array}{l}{a+b+c=1}\\{c=1}\\{9a+3b+c=2}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-\frac{5}{3}}\\{c=1}\end{array}\right.$,
故经过E、P、B三点的抛物线的解析式为y=$\frac{2}{3}$x2-$\frac{5}{3}$x+1.
点评 本题考查的是矩形的性质、相似三角形的判定和性质、二次函数的性质、待定系数法求二次函数解析式的知识以及坐标与图形的关系,正确运用数形结合思想、灵活运用相关定理和性质是解题的关键.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
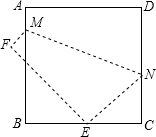 如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.
如图,将边长为8cm的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-1+x=(x+1)(x-1)+x | B. | (m+n)2-6(m+n)+9=(m+n-3)(m+n+3) | ||
| C. | x6-10x3-25=(x3-5)2 | D. | -1+x4=(x+1)(x-1)(x2+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
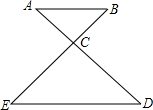 如图:已知△ABC∽△DEC,∠D=45°,∠ACB=60°,AC=3cm,BC=4cm,CE=6cm.求:
如图:已知△ABC∽△DEC,∠D=45°,∠ACB=60°,AC=3cm,BC=4cm,CE=6cm.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
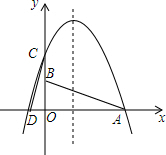 如图,已知,A点坐标是(3,0),B点坐标是(0,1),将△AOB绕点O逆时针旋转90°得到△COD,A、B旋转后的对应点分别为C和D,抛物线y=-x2+bx+c经过C、D两点.
如图,已知,A点坐标是(3,0),B点坐标是(0,1),将△AOB绕点O逆时针旋转90°得到△COD,A、B旋转后的对应点分别为C和D,抛物线y=-x2+bx+c经过C、D两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com