
【题目】如图,线段AB的端点在边长为1的小正方形网格的格点上,现将线段AB绕点A按逆时针方向旋转90°得到线段AC.

⑴请你在所给的网格中画出线段AC及点B经过的路径;
⑵若将此网格放在一平面直角坐标系中,已知点A的坐标为(1,3),点B的坐标为(-2, -1),则点C的坐标为 ;
⑶线段AB在旋转到线段AC的过程中,线段AB扫过的区域的面积为 ;
⑷若有一张与⑶中所说的区域形状相同的纸片,将它围成一个几何体的侧面,则该几何体底面圆的半径长为 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
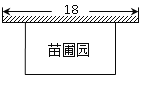
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
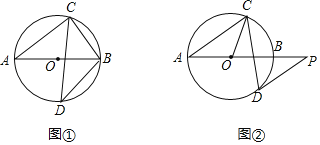
(1)如图①,若D为弧AB的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:
类比是数学中常用的数学思想.比如,我们可以类比多位数的加、减、乘、除的竖式运算方法,得到多项式与多项式的加、减、乘、除的运算方法.

理解应用:
(1)请仿照上面的竖式方法计算:![]() ;
;
(2)已知两个多项式的和为![]() ,其中一个多项式为
,其中一个多项式为![]() .请用竖式的方法求出另一个多项式.
.请用竖式的方法求出另一个多项式.
(3)已知一个长为![]() ,宽为
,宽为![]() 的矩形
的矩形![]() ,将它的长增加8.宽增加
,将它的长增加8.宽增加![]() 得到一个新矩形
得到一个新矩形![]() ,且矩形
,且矩形![]() 的周长是
的周长是![]() 周长的3倍(如图).同时,矩形
周长的3倍(如图).同时,矩形![]() 的面积和另一个一边长为
的面积和另一个一边长为![]() 的矩形
的矩形![]() 的面积相等,求
的面积相等,求![]() 的值和矩形
的值和矩形![]() 的另一边长.
的另一边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
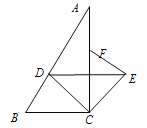
【题目】如图,在△ABC中,![]() ,CD平分
,CD平分![]() 交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上.
交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上.
(1)△CDB旋转了________度;
(2)连结DE,判断DE与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com