
【题目】已知等腰三角形ABC中,AB=AC,∠ABC=40°,P为直线BC上一点,PB=AB,则∠PAC=_____°.
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC的平分线AD和边BC的垂直平分线ED相交于点D,过点D作DF垂直于AC交AC的延长线于点F,若AB=8,AC=5,则CF=( )

A.1.5B.2C.2.5D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
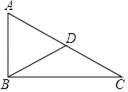
【题目】如图,在△ABC中,∠ABC=90°,BD为AC边上的中线.
(1)按如下要求尺规作图,保留作图痕迹,标注相应的字母:过点C作直线CE,使CE⊥BC于点C,交BD的延长线于点E,连接AE;
(2)求证:四边形ABCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC,AB=4,以AB为直径的半圆与BC边交于点D,过点D作DE⊥AC,垂足为E,过点E作EF⊥AB,垂足为F,连接FD.
(1)求证:DE是⊙O的切线;
(2)求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶叶公司经销一种茶叶,每千克成本为![]() 元,市场调查发现在一段时间内,销量
元,市场调查发现在一段时间内,销量![]() (千克)随销售单价
(千克)随销售单价![]() (元/千克)的变化而变化,具有关系为:
(元/千克)的变化而变化,具有关系为:![]() ,物价部门规定每千克的利润不得超过
,物价部门规定每千克的利润不得超过![]() 元.设这种茶叶在这段时间内的销售利润
元.设这种茶叶在这段时间内的销售利润![]() (元),解答下列问题:
(元),解答下列问题:
![]() 求
求![]() 与
与![]() 的关系式;
的关系式;
![]() 当
当![]() 取何值时,
取何值时,![]() 的值最大?并求出最大值;
的值最大?并求出最大值;
![]() 当销售利润
当销售利润![]() 的值最大时,销售额也是最大吗?判断并说明理由.
的值最大时,销售额也是最大吗?判断并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com