
【题目】如图,在△ABC中,∠BAC的平分线AD和边BC的垂直平分线ED相交于点D,过点D作DF垂直于AC交AC的延长线于点F,若AB=8,AC=5,则CF=( )

A.1.5B.2C.2.5D.3
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△AOB的边长为4,以O为坐标原点,OB所在直线为x轴建立如图所示的平面直角坐标系.

(1)求点A的坐标;
(2)若直线y=kx(k>0)与线段AB有交点,求k的取值范围;
(3)若点C在x轴正半轴上,以线段AC为边在第一象限内作等边△ACD,求直线BD的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)①已知直线l1:y=![]() x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有若干个白球和红球,这些球除颜色外都相同,某课外学习小组做摸球试验,将求搅均匀后从张任意摸出一个球,记下颜色后放回,搅匀,不断重复,获得数据如下
摸球次数 |
|
|
|
|
|
|
摸到白球的频数 |
|
|
|
|
|
|
摸到白球的频率 |
![]() 计算并填写表中摸到白球的频率;
计算并填写表中摸到白球的频率;
![]() 当摸球次数很大时,摸到的白球的频率估计值是多少?
当摸球次数很大时,摸到的白球的频率估计值是多少?
![]() 若已知袋中有白球
若已知袋中有白球![]() 个,试估计袋中红球的个数.
个,试估计袋中红球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球架的侧面示意图如图所示,现测得如下数据:底部支架AB的长为1.74m,后拉杆AE的倾斜角∠EAB=53°,篮板MN到立柱BC的水平距离BH=1.74m,在篮板MN另一侧,与篮球架横伸臂DG等高度处安装篮筐,已知篮筐到地面的距离GH的标准高度为3.05m.则篮球架横伸臂DG的长约为_____m(结果保留一位小数,参考数据:sin53°≈![]() , cos53°≈
, cos53°≈![]() ,tan53°≈
,tan53°≈![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
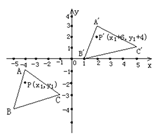
【题目】如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′ 的坐标。
(3)求△A′B′C′的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
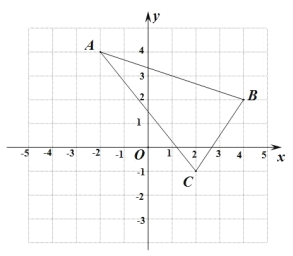
【题目】如图,△ABC 在平面直角坐标系中,点 A,B,C 的坐标分别为 A(-2,4),B(4,2),C(2,-1).
(Ⅰ)请在平面直角坐标系内,画出△ABC 关于 x 轴的对称图形△A1B1C1,其中,点 A,B,C 的对应点分别为A1,B1,C1;
(Ⅱ)请写出点C(2,-1)关于直线m(直线m上格点的横坐标都为-1)对称的点C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com