
【题目】(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)①已知直线l1:y=![]() x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.
【答案】⑴证明见解析;⑵y=-7x-21;⑶D(4,-2),(![]() ,
,![]() ).
).
【解析】
(1)根据△ABC为等腰直角三角形,AD⊥ED,BE⊥ED,可判定△ACD≌△CBE;
(2)①过点B作BC⊥AB,交l2于C,过C作CD⊥y轴于D,根据△CBD≌△BAO,得出BD=AO=3,CD=OB=4,求得C(-4,7),最后运用待定系数法求直线l2的函数表达式;
②根据△APD是以点D为直角顶点的等腰直角三角形,当点D是直线y=-2x+6上的动点且在第四象限时,分两种情况:当点D在矩形AOCB的内部时,当点D在矩形AOCB的外部时,设D(x,-2x+6),分别根据△ADE≌△DPF,得出AE=DF,据此列出方程进行求解即可.
(1)证明:如图1,
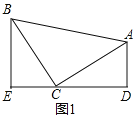
∵△ABC为等腰直角三角形,
∴CB=CA,∠ACD+∠BCE=90°,
又∵AD⊥ED,BE⊥ED,
∴∠D=∠E=90°,∠EBC+∠BCE=90°,
∴∠ACD=∠EBC,
在△ACD与△CBE中,
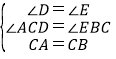 ,
,
∴△ACD≌△CBE(AAS);
(2)①如图2,过点B作BC⊥AB,交l2于C,过C作CD⊥y轴于D,
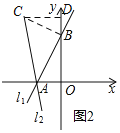
∵∠BAC=45°,
∴△ABC为等腰直角三角形,
由(1)可知:△CBD≌△BAO,
∴BD=AO,CD=OB,
∵直线l1:y=![]() x+4中,若y=0,则x=-3;若x=0,则y=4,
x+4中,若y=0,则x=-3;若x=0,则y=4,
∴A(-3,0),B(0,4),
∴BD=AO=3,CD=OB=4,
∴OD=4+3=7,
∴C(-4,7),
设l2的解析式为y=kx+b,则
![]() ,
,
解得![]() ,
,
∴l2的解析式:y=-7x-21;
②D(4,-2),(![]() ,
,![]() ).
).
理由:当点D是直线y=-2x+6上的动点且在第四象限时,分两种情况:
当点D在矩形AOCB的内部时,如图,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,
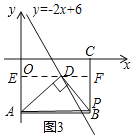
设D(x,-2x+6),则OE=2x-6,AE=6-(2x-6)=12-2x,DF=EF-DE=8-x,
由(1)可得,△ADE≌△DPF,则DF=AE,
即:12-2x=8-x,
解得x=4,
∴-2x+6=-2,
∴D(4,-2),
此时,PF=ED=4,CP=6=CB,符合题意;
当点D在矩形AOCB的外部时,如图,过D作x轴的平行线EF,交直线OA于E,交直线BC于F,
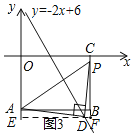
设D(x,-2x+6),则OE=2x-6,AE=OE-OA=2x-6-6=2x-12,DF=EF-DE=8-x,
同理可得:△ADE≌△DPF,则AE=DF,
即:2x-12=8-x,
解得x=![]() ,
,
∴-2x+6=-![]() ,
,
∴D(![]() ,-
,-![]() ),
),
此时,ED=PF=![]() ,AE=BF=
,AE=BF=![]() ,BP=PF-BF=
,BP=PF-BF=![]() <6,符合题意.
<6,符合题意.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形EFGH在边长为4的正方形ABCD所在平面上移动,始终保持EF//AB,CK=1.线段KG的中点为M,DH的中点为N,则线段MN的长为 ( ).

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天晚上,小春放学从学校步行回家,走了一段后,小春的同学小佳也从学校骑车回家,随后小佳追上了小春,并邀请小春坐他的自行车一起回家,但遭到了小春的拒绝.随后小佳便下车,推车与小春一起回家.很快小春到家了,小佳与小春道别后也骑上车继续回家.若学校、小春家、小佳家都在同一条笔直的公路上,则从小春出发时算起,小春与小佳的距离y关于时间t的函数图象最可能是下图中的( ).
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点且BE平分∠ABD,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
求证:
(1)∠BAD=2∠DAC
(2)EF=EG.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: 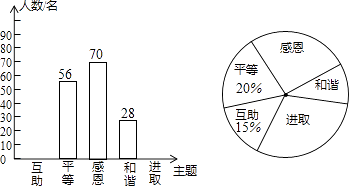
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com