Question

【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的5个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：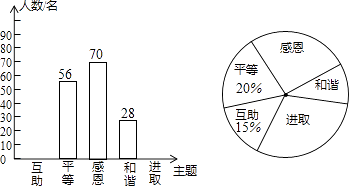
（1）这次调查的学生共有多少名？
（2）请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数．
（3）如果要在这5个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E）．

Answer 1

【答案】
（1）解：56÷20%=280（名），

答：这次调查的学生共有280名

（2）解：280×15%=42（名），280﹣42﹣56﹣28﹣70=84（名），

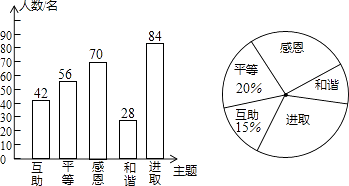
补全条形统计图，如图所示，

根据题意得：84÷280=30%，360°×30%=108°，

答：“进取”所对应的圆心角是108°

（3）解：由（2）中调查结果知：学生关注最多的两个主题为“进取”和“感恩”用列表法为：

	A	B	C	D	E
A		（A，B）	（A，C）	（A，D）	（A，E）
B	（B，A）		（B，C）	（B，D）	（B，E）
C	（C，A）	（C，B）		（C，D）	（C，E）
D	（D，A）	（D，B）	（D，C）		（D，E）
E	（E，A）	（E，B）	（E，C）	（E，D）

用树状图为：

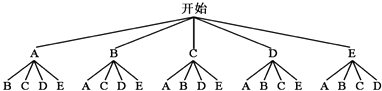
共20种情况，恰好选到“C”和“E”有2种，

∴恰好选到“进取”和“感恩”两个主题的概率是

【解析】（1）根据“平等”的人数除以占的百分比得到调查的学生总数即可；（2）求出“互助”与“进取”的学生数，补全条形统计图，求出“进取”占的圆心角度数即可；（3）列表或画树状图得出所有等可能的情况数，找出恰好选到“C”与“E”的情况数，即可求出所求的概率．