Question

【题目】已知等边△AOB的边长为4，以O为坐标原点，OB所在直线为x轴建立如图所示的平面直角坐标系．

（1）求点A的坐标；

（2）若直线y＝kx（k＞0）与线段AB有交点，求k的取值范围；

（3）若点C在x轴正半轴上，以线段AC为边在第一象限内作等边△ACD，求直线BD的解析式．

Answer 1

【答案】（1）点A的坐标为（2，2）；（2）0＜k≤；（3）y＝x﹣4

【解析】

（1）如下图所示，过点A作AD⊥x轴于点D，则AD＝OAsin∠AOB＝4sin60°＝2，同理OA＝2，即可求解；

（2）若直线y＝kx（k＞0）与线段AB有交点，当直线过点A时，将点A坐标代入直线的表达式得：2k＝2，解得：k＝，即可求解；

（3）证明△ACO≌△ADB（SAS），而∠DBC＝180°﹣∠ABO﹣∠ABD＝180°﹣60°﹣60°＝60°，即可求解．

解：（1）如下图所示，过点A作AD⊥x轴于点D，

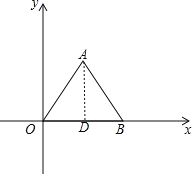
则AD＝OAsin∠AOB＝4sin60°＝，

同理OA＝2，

故点A的坐标为（2，2）；

（2）若直线y＝kx（k＞0）与线段AB有交点，

当直线过点A时，将点A坐标代入直线的表达式得：2k＝2，解得：k＝，

直线OB的表达式为：y＝0，而k＞0，

故：k的取值范围为：0＜k≤；

（3）如下图所示，连接BD，

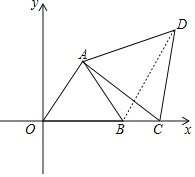
∵△OAB是等边三角形，∴AO＝AB，

∵△ADC为等边三角形，∴AD＝AC，

∠OAC＝∠OAB+∠CAB＝60°+∠CAB＝∠DAC+∠CAB＝∠DAB，

∴△ACO≌△ADB（SAS），

∴∠AOB＝∠ABD＝60°，

∴∠DBC＝180°﹣∠ABO﹣∠ABD＝180°﹣60°﹣60°＝60°，

故直线BD表达式的k值为tan60°=，

设直线BD的表达式为：y＝x+b，

将点B（4，0）代入上式得

解得：b＝﹣4，

故：直线BD的表达式为：y＝x﹣4．