
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() ,
,![]() ,
,![]() ,则由
,则由![]() ,
,![]() ,
,![]() 围成的图形(图中阴影部分)的面积为( )
围成的图形(图中阴影部分)的面积为( )

A. ![]() B. π C. 2π D. 4π
B. π C. 2π D. 4π
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图的△ABC中,AB>AC>BC,且D为BC上一点。现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等,以下是甲、乙两人的作法:
甲:连接AD,作AD的中垂线分别交AB、AC于P点、Q点,则P、Q两点即为所求;
乙:过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求;
对于甲、乙两人的作法,下列判断何者正确( )?

A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.


备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2013~2017年常住人口数统计如图所示.

根据图中提供的信息,回答下列问题:
(1)该市常住人口数,2017年比2016年增加了______万人;
(2)与上一年相比,该市常住人口数增加最多的年份是____________;
(3)预测2018年该市常住人口数大约为多少万人?请用所学的统计知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△AOB的边长为4,以O为坐标原点,OB所在直线为x轴建立如图所示的平面直角坐标系.

(1)求点A的坐标;
(2)若直线y=kx(k>0)与线段AB有交点,求k的取值范围;
(3)若点C在x轴正半轴上,以线段AC为边在第一象限内作等边△ACD,求直线BD的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)①已知直线l1:y=![]() x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
x+4与坐标轴交于点A、B,将直线l1绕点A逆时针旋转45o至直线l2,如图2,求直线l2的函数表达式;
②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
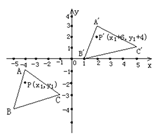
【题目】如图所示,△A′B′C′是△ABC经过平移得到的,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)。
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′ 的坐标。
(3)求△A′B′C′的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com