
【题目】如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.


备用图
【答案】(1)A2(4,0),B2(5,0),C2(5,2);(2)PP2=6.
【解析】试题分析:(1)根据关于y轴对称点的坐标特点是横坐标互为相反数,纵坐标相同可以得到△A1B1C1各点坐标,又关于直线l的对称图形点的坐标特点是纵坐标相同,横坐标之和等于3的二倍,由此求出△A2B2C1的三个顶点的坐标;
(2)P与P1关于y轴对称,利用关于y轴对称点的特点:纵坐标不变,横坐标变为相反数,求出P1的坐标,再由直线l的方程为直线x=3,利用对称的性质求出P2的坐标,即可PP2的长.
试题解析:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2);
(2)如图1,当0<a<3时,∵P与P1关于y轴对称,P(﹣a,0),∴P1(a,0),
又∵P1与P2关于l:直线x=3对称,
设P2(x,0),可得: ![]() =3,即x=6﹣a,
=3,即x=6﹣a,
∴P2(6﹣a,0),
则PP2=6﹣a﹣(﹣a)=6﹣a+a=6.



科目:初中数学 来源: 题型:
【题目】五一期间,青年旅行社组织一个团;老师和学生共50人组成的旅行团到凤凰古城旅游,景区门票售票标准是:成人门票50元/张,学生门票20元/张,该旅行团购买门票共花费1800元,若设该团购买成人门票x张,则可列方程为:____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.
(1) 乙先出发________h后,甲才出发;
(2) 请分别求出甲、乙的速度;并直接写出l1、、l2的表达式.
(3) 甲到达B地时,乙距B地还有多远?,乙还需几小时到达B地?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,部分同学准备开展社会实践活动,决定外出调研某名胜风景点的环境污染情况,为此需在风景点周边住一晚.某旅店只有二人间和三人间两种房型,二人间每晚需50元,三人间每晚需60元,并且二人间的数量不超过9间,三人间比二人间的房间数要少.有同学计算了一下,如果只住二人间,则还有5人无房可住,如果只住三人间,则只剩下1人没地方住.
(1)参加此次活动的同学有多少位?
(2)同学们此次住宿花费了430元,请你算算,同学租住的二人间和三人间各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
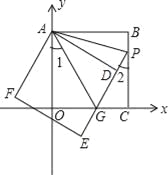
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(3,3).将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;
(3)当∠1=∠2时,求直线PE的解析式;
(4)在(3)的条件下,直线PE上是否存在点M,使以M、A、G为顶点的三角形是等腰三角形?若存在,请直接写出M点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com