
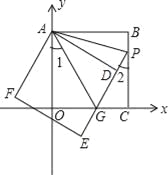
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCOЕФБпOAЁЂOCдкзјБъжсЩЯЃЌЕуBзјБъЮЊЃЈ3ЃЌ3ЃЉЃЎНЋе§ЗНаЮABCOШЦЕуAЫГЪБеыа§зЊНЧЖШІСЃЈ0ЁуЃМІСЃМ90ЁуЃЉЃЌЕУЕНе§ЗНаЮADEFЃЌEDНЛЯпЖЮOCгкЕуGЃЌEDЕФбгГЄЯпНЛЯпЖЮBCгкЕуPЃЌСЌAPЁЂAGЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїAOGЁеЁїADGЃЛ
ЃЈ2ЃЉЧѓЁЯPAGЕФЖШЪ§ЃЛВЂХаЖЯЯпЖЮOGЁЂPGЁЂBPжЎМфЕФЪ§СПЙиЯЕЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБЁЯ1=ЁЯ2ЪБЃЌЧѓжБЯпPEЕФНтЮіЪНЃЛ
ЃЈ4ЃЉдкЃЈ3ЃЉЕФЬѕМўЯТЃЌжБЯпPEЩЯЪЧЗёДцдкЕуMЃЌЪЙвдMЁЂAЁЂGЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіMЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)жЄУїЙ§ГЬМћНтЮіЃЛ(2)PG=OG+BPЃЛРэгЩМћНтЮіЃЛ(3)y=![]() xЉ3ЃЛ(4)ЃЈ0ЃЌЉ3ЃЉЛђЃЈ2
xЉ3ЃЛ(4)ЃЈ0ЃЌЉ3ЃЉЛђЃЈ2![]() ЃЌ3ЃЉЃЎ
ЃЌ3ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃК(1)гЩAO=ADЃЌAG=AGЃЌИљОнаББпКЭвЛЬѕжБНЧБпЖдгІЯрЕШЕФСНИіжБНЧШ§НЧаЮШЋЕШЃЌХаЖЯГіЁїAOGЁеЁїADGМДПЩЃЎ(2)ЪзЯШИљОнШ§НЧаЮШЋЕШЕФХаЖЈЗНЗЈЃЌХаЖЯГіЁїADPЁеЁїABPЃЌдйНсКЯЁїAOGЁеЁїADGЃЌПЩЕУЁЯDAP=ЁЯBAPЃЌЁЯ1=ЁЯDAGЃЛШЛКѓИљОнЁЯ1+ЁЯDAG+ЁЯDAP+ЁЯBAP=90ЁуЃЌЧѓГіЁЯPAGЕФЖШЪ§ЃЛзюКѓХаЖЯГіЯпЖЮOGЁЂPGЁЂBPжЎМфЕФЪ§СПЙиЯЕМДПЩЃЎ(3)ЪзЯШИљОнЁїAOGЁеЁїADGЃЌХаЖЯГіЁЯAGO=ЁЯAGDЃЛШЛКѓИљОнЁЯ1+ЁЯAGO=90ЁуЃЌЁЯ2+ЁЯPGC=90ЁуЃЌХаЖЯГіЕБЁЯ1=ЁЯ2ЪБЃЌЁЯAGO=ЁЯAGD=ЁЯPGCЃЌЖјЁЯAGO+ЁЯAGD+ЁЯPGC=180ЁуЃЌЧѓГіЁЯ1=ЁЯ2=30ЁуЃЛзюКѓШЗЖЈГіPЁЂGСНЕузјБъЃЌМДПЩХаЖЯГіжБЯпPEЕФНтЮіЪНЃЎ
(4)ИљОнЬтвтЃЌЗжСНжжЧщПіЃКЂйЕБЕуMдкxжсЕФИКАыжсЩЯЪБЃЛЂкЕБЕуMдкEPЕФбгГЄЯпЩЯЪБЃЛИљОнвдMЁЂAЁЂGЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌЧѓГіMЕузјБъЪЧЖрЩйМДПЩЃЎ
ЪдЬтНтЮіЃК(1)дкRtЁїAOGКЭRtЁїADGжаЃЌ![]() ЃЈHLЃЉ ЁрЁїAOGЁеЁїADGЃЎ
ЃЈHLЃЉ ЁрЁїAOGЁеЁїADGЃЎ
(2)дкRtЁїADPКЭRtЁїABPжаЃЌ![]() ЁрЁїADPЁеЁїABPЃЌ дђЁЯDAP=ЁЯBAPЃЛ
ЁрЁїADPЁеЁїABPЃЌ дђЁЯDAP=ЁЯBAPЃЛ
ЁпЁїAOGЁеЁїADGЃЌ ЁрЁЯ1=ЁЯDAGЃЛ гжЁпЁЯ1+ЁЯDAG+ЁЯDAP+ЁЯBAP=90ЁуЃЌ
Ёр2ЁЯDAG+2ЁЯDAP=90ЁуЃЌ ЁрЁЯDAG+ЁЯDAP=45ЁуЃЌ ЁпЁЯPAG=ЁЯDAG+ЁЯDAPЃЌ ЁрЁЯPAG=45ЁуЃЛ
ЁпЁїAOGЁеЁїADGЃЌ ЁрDG=OGЃЌ ЁпЁїADPЁеЁїABPЃЌ ЁрDP=BPЃЌ ЁрPG=DG+DP=OG+BPЃЎ
(3)НтЃКЁпЁїAOGЁеЁїADGЃЌ ЁрЁЯAGO=ЁЯAGDЃЌ гжЁпЁЯ1+ЁЯAGO=90ЁуЃЌЁЯ2+ЁЯPGC=90ЁуЃЌЁЯ1=ЁЯ2ЃЌ
ЁрЁЯAGO=ЁЯPGCЃЌ гжЁпЁЯAGO=ЁЯAGDЃЌ ЁрЁЯAGO=ЁЯAGD=ЁЯPGCЃЌ
гжЁпЁЯAGO+ЁЯAGD+ЁЯPGC=180ЁуЃЌ ЁрЁЯAGO=ЁЯAGD=ЁЯPGC=180ЁуЁТ3=60ЁуЃЌ
ЁрЁЯ1=ЁЯ2=90ЁуЉ60Ёу=30ЁуЃЛ дкRtЁїAOGжаЃЌ ЁпAO=3ЃЌ ЁрOG=AOtan30Ёу=3ЁС![]() =
=![]() ЃЌ
ЃЌ
ЁрGЕузјБъЮЊЃЈ![]() ЃЌ0ЃЉЃЌCG=3Љ
ЃЌ0ЃЉЃЌCG=3Љ![]() ЃЌ дкRtЁїPCGжаЃЌPC=
ЃЌ дкRtЁїPCGжаЃЌPC=![]() =
=![]() =3ЃЈ
=3ЃЈ![]() Љ1ЃЉЃЌ
Љ1ЃЉЃЌ
ЁрPЕузјБъЮЊЃКЃЈ3ЃЌ3![]() Љ3 ЃЉЃЌ ЩшжБЯпPEЕФНтЮіЪНЮЊЃКy=kx+bЃЌ дђ
Љ3 ЃЉЃЌ ЩшжБЯпPEЕФНтЮіЪНЮЊЃКy=kx+bЃЌ дђ ЃЌ
ЃЌ
НтЕУЃК ЃЌ ЁржБЯпPEЕФНтЮіЪНЮЊy=
ЃЌ ЁржБЯпPEЕФНтЮіЪНЮЊy=![]() xЉ3ЃЎ
xЉ3ЃЎ
(4)ЂйШчЭМ/span>1ЃЌЕБЕуMдкxжсЕФИКАыжсЩЯЪБЃЌЃЌ ЁпAG=MGЃЌЕуAзјБъЮЊЃЈ0ЃЌ3ЃЉЃЌ
ЁрЕуMзјБъЮЊЃЈ0ЃЌЉ3ЃЉЃЎ


ЂкШчЭМ2ЃЌЕБЕуMдкEPЕФбгГЄЯпЩЯЪБЃЌЃЌ гЩЃЈ3ЃЉЃЌПЩЕУЁЯAGO=ЁЯPGC=60ЁуЃЌ
ЁрEPгыABЕФНЛЕуMЃЌТњзуAG=MGЃЌ ЁпAЕуЕФКсзјБъЪЧ0ЃЌGЕуКсзјБъЮЊ![]() ЃЌ
ЃЌ
ЁрMЕФКсзјБъЪЧ2![]() ЃЌзнзјБъЪЧ3ЃЌ ЁрЕуMзјБъЮЊЃЈ2
ЃЌзнзјБъЪЧ3ЃЌ ЁрЕуMзјБъЮЊЃЈ2![]() ЃЌ3ЃЉЃЎ
ЃЌ3ЃЉЃЎ
злЩЯЃЌПЩЕУ ЕуMзјБъЮЊЃЈ0ЃЌЉ3ЃЉЛђЃЈ2![]() ЃЌ3ЃЉЃЎ
ЃЌ3ЃЉЃЎ


 ЮФОДЭМЪщПЮЪБЯШЗцЯЕСаД№АИ
ЮФОДЭМЪщПЮЪБЯШЗцЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпlЙ§ЕуMЃЈ3ЃЌ0ЃЉЃЌЧвЦНаагкyжсЃЎ
ЃЈ1ЃЉШчЙћЁїABCШ§ИіЖЅЕуЕФзјБъЗжБ№ЪЧAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉЃЌCЃЈЉ1ЃЌ2ЃЉЃЌЁїABCЙигкyжсЕФЖдГЦЭМаЮЪЧЁїA1B1C1ЃЌЁїA1B1C1ЙигкжБЯпlЕФЖдГЦЭМаЮЪЧЁїA2B2C2ЃЌаДГіЁїA2B2C2ЕФШ§ИіЖЅЕуЕФзјБъЃЛ
ЃЈ2ЃЉШчЙћЕуPЕФзјБъЪЧЃЈЉaЃЌ0ЃЉЃЌЦфжа0ЃМaЃМ3ЃЌЕуPЙигкyжсЕФЖдГЦЕуЪЧP1ЃЌЕуP1ЙигкжБЯпlЕФЖдГЦЕуЪЧP2ЃЌЧѓPP2ЕФГЄЃЎ


БИгУЭМ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪа5дТЕФФГвЛжмУПЬьЕФзюИпЦјЮТЃЈЕЅЮЛЃКЁцЃЉЭГМЦШчЯТЃК19ЃЌ20ЃЌ24ЃЌ22ЃЌ24ЃЌ26ЃЌ27ЃЌдђетзщЪ§ОнЕФжаЮЛЪ§гыжкЪ§ЗжБ№ЪЧЃЈ ЃЉ
A.23ЃЌ24
B.24ЃЌ22
C.24ЃЌ24
D.22ЃЌ24
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПСЩФўКХКНПеФИНЂЪЧжаЙњШЫУёНтЗХОќКЃОќЕквЛЫвЗўвлЕФКНПеФИНЂЃЎТњдиЪБХХЫЎСПЮЊ67500ЖжЃЌНЋЪ§Он67500гУПЦбЇМЧЪ§ЗЈБэЪОЮЊЃЈЁЁЁЁЃЉ
A.6.75ЁС103B.6.75ЁС104C.0.675ЁС105D.675ЁС102
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФвЛдЊЖўДЮЗНГЬx2-4x+mЃН0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌдђЪЕЪ§mЕФШЁжЕЗЖЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁРђЕФАжАжТђСЫФГбнГЊЛсЕФвЛеХУХЦБЃЌЫ§КЭИчИчСНШЫЖМКмЯыШЅЙлПДЃЌПЩУХЦБжЛгавЛеХЃЌЖСОХФъМЖЕФИчИчЯыСЫвЛИіАьЗЈЃЌФУСЫАЫеХЦЫПЫХЦЃЌНЋЪ§зжЮЊ1ЃЌ2ЃЌ3ЃЌ5ЕФЫФеХХЦИјаЁРђЃЌНЋЪ§зжЮЊ4ЃЌ6ЃЌ7ЃЌ8ЕФЫФеХХЦСєИјздМКЃЌВЂАДШчЯТгЮЯЗЙцдђНјааЃКаЁРђКЭИчИчДгИїздЕФЫФеХХЦжаЫцЛњГщГівЛеХЃЌШЛКѓНЋГщГіЕФСНеХХЦЪ§зжЯрМгЃЌШчЙћКЭЮЊХМЪ§ЃЌдђаЁРђШЅЃЛШчЙћКЭЮЊЦцЪ§ЃЌдђИчИчШЅЃЎ
ЃЈ1ЃЉЧыгУЪїзДЭМЛђСаБэЕФЗНЗЈБэЪОГіСНеХХЦЪ§зжЯрМгКЭЕФЫљгаПЩФмГіЯжЕФНсЙћЃЛ
ЃЈ2ЃЉИчИчЩшМЦЕФгЮЯЗЙцдђЙЋЦНТ№ЃПЮЊЪВУДЃПШєВЛЙЋЦНЃЌЧыЩшМЦвЛжжЙЋЦНЕФгЮЯЗЙцдђЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћНЋХзЮяЯпyЃНx2+2ЯђзѓЦНвЦ1ИіЕЅЮЛЃЌФЧУДЫљЕУаТХзЮяЯпЕФНтЮіЪНЮЊЃЈЁЁЁЁЃЉ
A.yЃНЃЈxЉ1ЃЉ2+2B.yЃНЃЈx+1ЃЉ2+2C.yЃНx2+1D.yЃНx2+3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABOжаЃЌABЁЭOBЃЌOB=![]() ЃЌAB=1ЃЌАбЁїABOШЦЕуOа§зЊ150ЁуКѓЕУЕНЁїA1B1OЃЌдђЕуA1ЕФзјБъЮЊЃЈ ЃЉ
ЃЌAB=1ЃЌАбЁїABOШЦЕуOа§зЊ150ЁуКѓЕУЕНЁїA1B1OЃЌдђЕуA1ЕФзјБъЮЊЃЈ ЃЉ
AЃЎЃЈЉ1ЃЌ-![]() ЃЉ
ЃЉ
BЃЎЃЈЉ1ЃЌ-![]() ЃЉЛђЃЈЉ2ЃЌ0ЃЉ
ЃЉЛђЃЈЉ2ЃЌ0ЃЉ
CЃЎЃЈ-![]() ЃЌЉ1ЃЉЛђЃЈ0ЃЌЉ2ЃЉ
ЃЌЉ1ЃЉЛђЃЈ0ЃЌЉ2ЃЉ
DЃЎЃЈ-![]() ЃЌЉ1ЃЉ
ЃЌЉ1ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЫљЪОЪЧвЛИіГЄЮЊ2mЃЌПэЮЊ2nЕФГЄЗНаЮЃЌбиЭМжаащЯпгУМєЕЖОљЗжГЩЫФИіаЁГЄЗНаЮЃЌЭМЂкЪЧБпГЄЮЊmЃnЕФе§ЗНаЮЃЎ
ЃЈ1ЃЉЧыгУЭМЂйжаЫФИіаЁГЄЗНаЮКЭЭМЂкжаЕФе§ЗНаЮЦДГЩвЛИіДѓе§ЗНаЮЃЌЛГіЪОвтЭМ(вЊЧѓСЌНгДІМШУЛгажиЕўЃЌвВУЛгаПеЯЖ)ЃЛ
ЃЈ2ЃЉЧыгУСНжжВЛЭЌЕФЗНЗЈСаДњЪ§ЪНБэЪО(1)жаЦДЕУЕФДѓе§ЗНаЮЕФУцЛ§ЃЛ
ЃЈ3ЃЉЧыжБНгаДГі(mЃЋn)2ЃЌ(mЃn)2ЃЌmnетШ§ИіДњЪ§ЪНжЎМфЕФЕШСПЙиЯЕЃЛ
ЃЈ4ЃЉИљОнЃЈ4ЃЉжаЕФЕШСПЙиЯЕЃЌНтОіШчЯТЮЪЬтЃКШєaЃЋbЃН6ЃЌabЃН4ЃЌЧѓ(aЃb)2ЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com