
【题目】如图,顶点为P(4,﹣4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON,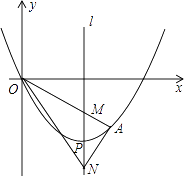
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,﹣3),求△ANO的面积;
(3)若点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
【答案】
(1)
解:∵二次函数的顶点坐标为(4,﹣4),
∴设二次函数的解析式为y=a(x﹣4)2﹣4,
又二次函数过(0,0),
∴0=a(0﹣4)2﹣4,解得:a= ![]() ,
,
∴二次函数解析式为y= ![]() (x﹣4)2﹣4=
(x﹣4)2﹣4= ![]() x2﹣2x
x2﹣2x
(2)
解:设直线OA的解析式为y=kx,将A(6,﹣3)代入得﹣3=6k,解得k=﹣ ![]() ,
,
∴直线OA的解析式为y=﹣ ![]() x,
x,
把x=4代入y=﹣ ![]() x得y=﹣2,
x得y=﹣2,
∴M(4,﹣2),
又∵点M、N关于点P对称,
∴N(4,﹣6),
∴MN=4,
∴S△ANO= ![]() ×6×4=12
×6×4=12
(3)
解:①证明:过A作AH⊥l于H,l与x轴交于点D,如图所示:
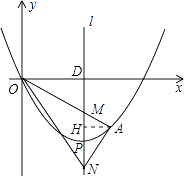
设A(m, ![]() m2﹣2m),又O(0,0),
m2﹣2m),又O(0,0),
∴直线AO的解析式为y= ![]() x=(
x=( ![]() m﹣2)x,
m﹣2)x,
则M(4,m﹣8),N(4,﹣m),H(4, ![]() m2﹣2m),
m2﹣2m),
∴OD=4,ND=m,HA=m﹣4,NH=ND﹣HD= ![]() m2﹣m,
m2﹣m,
在Rt△OND中,tan∠ONM= ![]() =
= ![]() ,
,
在Rt△ANH中,tan∠ANM= ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴tan∠ONM=tan∠ANM,
则∠ANM=∠ONM;
②△ANO能为直角三角形,理由如下:
分三种情况考虑:
(i)若∠ONA为直角,由①得:∠ANM=∠ONM=45°,
∴△AHN为等腰直角三角形,
∴HA=NH,即m﹣4= ![]() m2﹣m,
m2﹣m,
整理得:m2﹣8m+16=0,即(m﹣4)2=0,
解得:m=4,
此时点A与点P重合,故不存在A点使△ONA为直角三角形;
(ii)若∠AON为直角,根据勾股定理得:OA2+ON2=AN2,
∵OA2=m2+( ![]() m2﹣2m)2,ON2=42+m2,AN2=(m﹣4)2+(
m2﹣2m)2,ON2=42+m2,AN2=(m﹣4)2+( ![]() m2﹣2m+m)2,
m2﹣2m+m)2,
∴m2+( ![]() m2﹣2m)2+42+m2=(m﹣4)2+(
m2﹣2m)2+42+m2=(m﹣4)2+( ![]() m2﹣2m+m)2,
m2﹣2m+m)2,
整理得:m(m2﹣8m﹣16)=0,
解得:m=0或m=4+4 ![]() 或4﹣4
或4﹣4 ![]() (舍去),
(舍去),
当m=0时,A点与原点重合,故∠AON不能为直角,
当m=4+4 ![]() ,即A(4+4
,即A(4+4 ![]() ,4)时,N为第四象限点,成立,故∠AON能为直角;
,4)时,N为第四象限点,成立,故∠AON能为直角;
(iii)若∠NAO为直角,可得∠NAM=∠ODM=90°,且∠AMN=∠DMO,
∴△AMN∽△DMO,
又∠MAN=∠ODN=90°,且∠ANM=∠OND,
∴△AMN∽△DON,
∴△AMN∽△DMO∽△DON,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
整理得:(m﹣4)2=0,
解得:m=4,
此时A与P重合,故∠NAO不能为直角,
综上,点A在对称轴l右侧的二次函数图象上运动时,△ANO能为直角三角形,当m=4+4 ![]() ,即A(4+4
,即A(4+4 ![]() ,4)时,N为第四象限点,成立,故∠AON能为直角
,4)时,N为第四象限点,成立,故∠AON能为直角
【解析】(1)由二次函数的顶点坐标,设出二次函数的顶点式,再由二次函数过原点,将原点坐标代入设出的解析式中,确定出a的值,即可求出二次函数的解析式;(2)首先通过求出OA直线方程求出M点的坐标,再通过对称性求出N点的坐标,进而求出MN的长度,△ANO的面积可以通过A点的横坐标长度和MN的长度计算得到;(3)①过A作AH垂直于直线l,直线l与x轴交于点D,由A在二次函数图象上,设A横坐标为m,将x=m代入二次函数解析式,表示出纵坐标,确定出A的坐标,再由O的坐标,表示出直线AO的解析式,进而表示出M,N及H的坐标,得出OD,ND,HA,及NH,在直角三角形OND中,利用锐角三角函数定义表示出tan∠ONM,在直角三角形ANH中,利用锐角三角函数定义表示出tan∠ANM,化简后得到tan∠ONM=tan∠ANM,可得出∠ONM=∠ANM,得证;
②△ANO不能为直角三角形,理由为:分三种情况考虑:若∠ONA为直角,由①得到∠ANM=∠ONM=45°,可得出三角形AHN为等腰直角三角形,得到AH=HN,将表示出的AH及HN代入,得到关于m的方程,求出方程的解得到m的值为0或4± ![]() ,进而得到此时A与P重合,不合题意,故∠ONA不能为直角;若∠AON为直角,利用勾股定理得到OA2+ON2=AN2 , 由A的坐标,利用勾股定理表示出OA2 , 由OD及DN,利用勾股定理表示出ON2 , 由AH及HN,利用勾股定理表示出AN2 , 代入OA2+ON2=AN2 , 得到关于m的方程,求出方程的解得到m的值为4±4
,进而得到此时A与P重合,不合题意,故∠ONA不能为直角;若∠AON为直角,利用勾股定理得到OA2+ON2=AN2 , 由A的坐标,利用勾股定理表示出OA2 , 由OD及DN,利用勾股定理表示出ON2 , 由AH及HN,利用勾股定理表示出AN2 , 代入OA2+ON2=AN2 , 得到关于m的方程,求出方程的解得到m的值为4±4 ![]() 或0,然后判断∠AON是否为直角;若∠NAO为直角,则有△AMN∽△DMO∽△DON,由相似得比例,将各自的值代入得到关于m的方程,求出方程的解得到m的值为4,此时A与P重合,故∠NAO不能为直角,综上,点A在对称轴l右侧的二次函数图象上运动时,△ANO不能为直角三角形.
或0,然后判断∠AON是否为直角;若∠NAO为直角,则有△AMN∽△DMO∽△DON,由相似得比例,将各自的值代入得到关于m的方程,求出方程的解得到m的值为4,此时A与P重合,故∠NAO不能为直角,综上,点A在对称轴l右侧的二次函数图象上运动时,△ANO不能为直角三角形.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】解答题
(1)如图(1)点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E在BC的延长线上,且CE=CP,连接BP,DE.求证:△BCP≌△DCE; 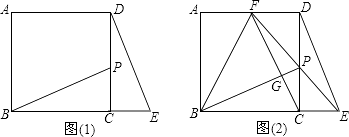
(2)直线EP交AD于F,连接BF,FC.点G是FC与BP的交点. ①若CD=2PC时,求证:BP⊥CF;
②若CD=nPC(n是大于1的实数)时,记△BPF的面积为S1 , △DPE的面积为S2 . 求证:S1=(n+1)S2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知△ABC和△DEF的顶点坐标分别为A(1,0)、B(3,0)、C(2,1)、D(4,3)、E(6,5)、F(4,7).
按下列要求画图:以O为位似中心,将△ABC向y轴左侧按比例尺2:1放大得△ABC的位似图形△A1B1C1 , 并解决下列问题:
(1)顶点A1的坐标为 , B1的坐标为 , C1的坐标为;
(2)请你利用旋转、平移两种变换,使△A1B1C1通过变换后得到△A2B2C2 , 且△A2B2C2恰与△DEF拼接成一个平行四边形(非正方形),写出符合要求的变换过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B与∠C的平分线交于点O,过点O作DE∥BC,分别交AB、AC于点D、E.若AB=5,AC=4,则△ADE的周长是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=3,OC=2,点F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= ![]() 的图象与BC边交于点E.
的图象与BC边交于点E. 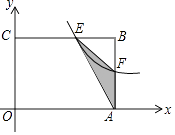
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同,其中黄球的个数是白球个数的2倍少5个,已知从袋中摸出一个红球的概率是 ![]() .
.
(1)求袋中红球的个数;
(2)求从袋中摸出一个球是白球的概率;
(3)取走5个黄球5个白球,求从剩余的球中摸出一个球是红球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com