
【题目】如图,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0) , 且x1+x2=4, ![]() .
.

(1)求抛物线的代数表达式;
(2)设抛物线与y轴交于C点,求直线BC的表达式;
(3)求△ABC的面积.
【答案】(1)该抛物线的代数表达式为y=-x2+4x-3;(2)直线BC的代数表达式为y=x-3;(3)S△ABC=3.
【解析】试题分析:(1)先解方程组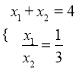 , 求得x1、x2的值,再代入抛物线y=-x2+bx+c即可求得抛物线的代数表达式;
, 求得x1、x2的值,再代入抛物线y=-x2+bx+c即可求得抛物线的代数表达式;
(2)设直线BC的表达式为y=kx+m,先求得抛物线与y轴的交点坐标,再根据待定系数法即可求得直线BC的表达式;
(3)分别求出AB、OC的长,再根据三角形的面积公式即可求得结果.
(1)解方程组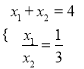 , 得x1=1,x2=3.
, 得x1=1,x2=3.
故![]() ,解这个方程组,得b=4,c=-3.
,解这个方程组,得b=4,c=-3.
所以,该抛物线的代数表达式为y=-x2+4x-3.
(2)设直线BC的表达式为y=kx+m.
由(1)得,当x=0时,y=-3,故C点坐标为(0,-3).
所以![]() ,解得
,解得![]()
∴直线BC的代数表达式为y=x-3
(3)由于AB=3-1=2,OC=│-3│=3.
故S△ABC=![]() AB·OC=
AB·OC=![]() ×2×3=3.
×2×3=3.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽取20袋,检测每袋的质量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
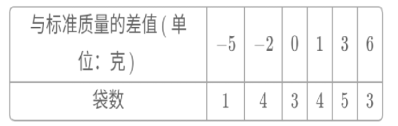
(1)这批样品的质量比标准质量多还是少?多或少几克?
(2)若每袋标准质量为450克,则抽样检测的总质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(﹣2,6),C(2,2)两点.
(1)记抛物线顶点为D,求△BCD的面积;
(2)若直线y=﹣![]() x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.
x向上平移b个单位所得的直线与抛物线段BDC(包括端点B、C)部分有两个交点,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,数轴上三个点A、O、P,点O是原点,固定不动,点A和B可以移动,点A表示的数为![]() ,点B表示的数为
,点B表示的数为![]() .
.
(1)若A、B移动到如图所示位置,计算![]() 的值.
的值.
(2)在(1)的情况下,B点不动,点A向左移动3个单位长,写出A点对应的数![]() ,并计算
,并计算![]() .
.
(3)在(1)的情况下,点A不动,点B向右移动15.3个单位长,此时![]() 比
比![]() 大多少?请列式计算.
大多少?请列式计算.
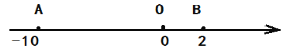
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数![]() 和
和![]() 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥
的图象上,PC⊥![]() 轴于点C,交
轴于点C,交![]() 的图象于点A,PC⊥
的图象于点A,PC⊥![]() 轴于点D,交
轴于点D,交![]() 的图象于点B. 当点P在
的图象于点B. 当点P在![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①![]()
②![]() 的值不会发生变化
的值不会发生变化
③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y= -x2-2x的图象与x轴交于点A、O,在抛物线上有一点P,满足
S△AOP=3,则点P的坐标是( )
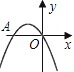
A. (-3,-3) B. (1,-3) C. (-3,-3)或(-3,1) D. (-3,-3)或(1,-3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在活动课上,小明和小红合作用一副三角板来测量学校旗杆高度.已知小明的眼睛与地面的距离(AB)是1.7m,他调整自己的位置,设法使得三角板的一条直角边保持水平,且斜边与旗杆顶端M在同一条直线上,测得旗杆顶端M仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,用同样的方法测得旗杆顶端M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).求出旗杆MN的高度.(参考数据: ![]() ,结果保留整数.)
,结果保留整数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,∠AOB和∠COD都是直角,请你写出∠AOD和∠BOC之间的数量关系,并说明理由;
(2)当∠COD绕点O旋转到如图②所示的位置时,上述结论还成立吗?并说明理由;
(3)如图③,当∠AOB=∠COD=β(0°<β<90°)时,请你直接写出∠AOD和∠BOC之间的数量关系.(不用说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
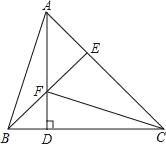
【题目】已知:如图,△ABC中,∠ACB=45°,AD⊥BC于D,CF交AD于点F,连接BF并延长交AC于点E,∠BAD=∠FCD.求证:
(1)△ABD≌△CFD;
(2)BE⊥AC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com