
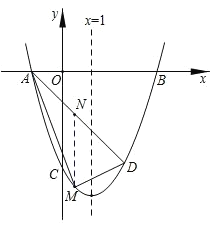
【题目】如图,抛物线y=x2+bx+c与x轴交于A,B两点(A在B的左侧),与y轴交于点C(0,﹣3),对称轴为x=1,点D与C关于抛物线的对称轴对称.
(1)求抛物线的解析式及点D的坐标;
(2)点P是抛物线上的一点,当△ABP的面积是8时,求出点P的坐标;
(3)点M为直线AD下方抛物线上一动点,设点M的横坐标为m,当m为何值时,△ADM的面积最大?并求出这个最大值.

【答案】(1)y=x2﹣2x﹣3,D(2,﹣3);(2)P(1﹣2![]() ,4)或(1+2
,4)或(1+2![]() ,4)或(1,﹣4);(3)m=
,4)或(1,﹣4);(3)m=![]() 时,△AMD的最大值为
时,△AMD的最大值为![]()
【解析】
(1)由抛物线y=x2+bx+c的对称轴为x=1,求出b的值,再由点C的坐标求出c的值即可;
(2)先求出点A,点B的坐标,设点P的坐标为(s,t),因为△ABP的面积是8,根据三角形的面积公式可求出t的值,再将t的值代入抛物线解析式即可;
(3)求出直线AD的解析式,过点M作MN∥y轴,交AD于点N,则点M的坐标为(m,m2﹣2m﹣3),点N的坐标为(m,﹣m﹣1),用含m的代数式表示出△AMN的面积,配方后由二次函数的性质即可得出结论.
(1)∵抛物线y=x2+bx+c的对称轴为x=1,
∴![]() 1,
1,
∴b﹣=2.
∵抛物线与y轴交于点C(0,﹣3),
∴c=﹣3,
∴抛物线的解析式为y=x2﹣2x﹣3,
∴抛物线的对称轴为直线x=1.
∵点D与C关于抛物线的对称轴对称,
∴点D的坐标为(2,﹣3);
(2)当y=0时,x2﹣2x﹣3=0,
解得:x1=﹣1,x2=3,
∴点A的坐标为(﹣1,0),点B的坐标为(3,0),
∴AB=3﹣(﹣1)=4,
设点P的坐标为(s,t).
∵△ABP的面积是8,
∴![]() AB|yP|=8,
AB|yP|=8,
即![]() 4|t|=8,
4|t|=8,
∴t=±4,
①当t=4时,s2﹣2s﹣3=4,
解得:,s1=![]() ,s2=
,s2=![]() ,
,
∴点P的坐标为(![]() ,4)或(
,4)或(![]() ,4);
,4);
②当t=﹣4时,s2﹣2s﹣3=﹣4,
解得:,s1=s
∴点P的坐标为(1,﹣4);
综上所述:当△ABP的面积是8时,点P的坐标为(![]() ,4)或(
,4)或(![]() ,4)或(1,﹣4);
,4)或(1,﹣4);
(3)设直线AD的解析式为y=kx+b1,
将A(﹣1,0),D(2,﹣3)代入y=kx+b1,
得: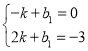 ,
,
解得: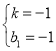 ,
,
∴直线AD的解析式为y=﹣x﹣1,
过点M作MN∥y轴,交AD于点N.
∵点M的横坐标是m(﹣1<m<2),
∴点M的坐标为(m,m2﹣2m﹣3),点N的坐标为(m,﹣m﹣1),
∴MN=﹣m﹣1﹣(m2﹣2m﹣3)=﹣m2+m+2,
∴S△AMD=S△AMN+S△DMN
![]() MN(m+1)
MN(m+1)![]() MN(2﹣m)
MN(2﹣m)
![]() MN
MN
![]() (﹣m2+m+2)
(﹣m2+m+2)
![]() (m
(m![]() )2
)2![]() ,
,
∵![]() 0,﹣1
0,﹣1![]() 2,
2,
∴当m![]() 时,S△AMD
时,S△AMD![]() ,
,
∴当m![]() 时,△AMD的最大值为
时,△AMD的最大值为![]() .
.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的学习材料:
我们知道,一般情况下式子![]() 与“
与“![]() ”是不相等的(m,n均为整数),但当m,n取某些特定整数时,可以使这两个式子相等,我们把使“
”是不相等的(m,n均为整数),但当m,n取某些特定整数时,可以使这两个式子相等,我们把使“![]() =
=![]() ”成立的数对“m,n”叫做“好数对”,记作[m,n],例如,当m=n=0时,有
”成立的数对“m,n”叫做“好数对”,记作[m,n],例如,当m=n=0时,有![]() =
=![]() 成立,则数对“0,0”就是一对“好数对”,记作[0,0]
成立,则数对“0,0”就是一对“好数对”,记作[0,0]
解答下列问题:
(1)通过计算,判断数对“3,4”是否是“好数对”;
(2)求“好数对”[x,﹣32]中x的值;
(3)请再写出一对上述未出现的“好数对”[ , ];
(4)对于“好数对[a,b],如果a=9k(k为整数),则b= (用含k的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
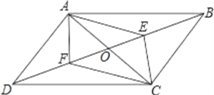
【题目】如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E,F分别是OB,OD的中点.
(1)试说明四边形AECF是平行四边形.
(2)若AC=8,AB=6.若AC⊥AB,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
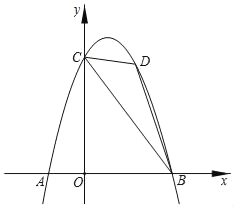
【题目】如图,抛物线y=ax2+bx+6经过点A(﹣2,0),B(4,0)两点,与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为m(1<m<4)连接BC,DB,DC.
(1)求抛物线的函数解析式;
(2)△BCD的面积是否存在最大值,若存在,求此时点D的坐标;若不存在,说明理由;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
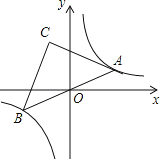
【题目】如图,反比例函数y=![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=![]() 的图象上运动,tan∠CAB=2,则k=_____.
的图象上运动,tan∠CAB=2,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
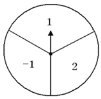
【题目】如图,一转盘被等分成三个扇形,上面分别标有-1,1,2中的一个数,指针固定,转动转盘后任其自由停止,这时某个扇形会恰好停在指针所指的位置,并相应得到这个扇形上的数( 若指针恰好指在等分线上,当做指向右边的扇形).若转动一次转盘,将所得的数作为k,则使反比例函数![]() 的图象在第一、三象限的概率是多少?若小静和小宇进行游戏,每人各转动两次转盘,若两次所得数的积为正数,则小静赢,若两次所得数的积为负数,则小宇赢.这是个公平的游戏吗?请说明理由.(借助画树状图或列表的方法)
的图象在第一、三象限的概率是多少?若小静和小宇进行游戏,每人各转动两次转盘,若两次所得数的积为正数,则小静赢,若两次所得数的积为负数,则小宇赢.这是个公平的游戏吗?请说明理由.(借助画树状图或列表的方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三辆汽车经过某收费站下高速时,在2个收费通道A,B中,可随机选择其中的一个通过.
(1)三辆汽车经过此收费站时,都选择A通道通过的概率是 ;
(2)求三辆汽车经过此收费站时,至少有两辆汽车选择B通道通过的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
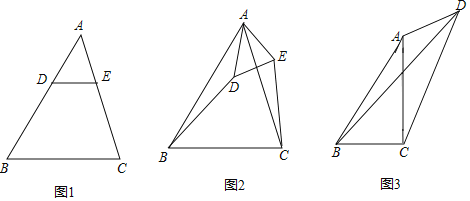
【题目】(1)如图1,在△ABC中,AB>AC,点D,E分别在边AB,AC上,且DE∥BC,若AD=2,AE=![]() ,则
,则![]() 的值是 ;
的值是 ;
(2)如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE和BD,![]() 的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
(3)如图3,在四边形ABCD中,AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ=![]() ,当CD=6,AD=3时,请直接写出线段BD的长度.
,当CD=6,AD=3时,请直接写出线段BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com