
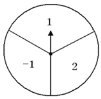
����Ŀ����ͼ��һת�̱��ȷֳ��������Σ�����ֱ����-1��1��2�е�һ������ָ��̶���ת��ת�̺���������ֹͣ����ʱij�����λ�ǡ��ͣ��ָ����ָ��λ�ã�����Ӧ�õ���������ϵ����� ��ָ��ǡ��ָ�ڵȷ����ϣ�����ָ���ұߵ����Σ�����ת��һ��ת�̣������õ�����Ϊk����ʹ����������![]() ��ͼ���ڵ�һ�������ĸ����Ƕ��٣���С����С�������Ϸ��ÿ�˸�ת������ת�̣��������������Ļ�Ϊ��������С��Ӯ���������������Ļ�Ϊ��������С��Ӯ�����Ǹ���ƽ����Ϸ����˵�����ɣ�����������״ͼ���б��ķ�����
��ͼ���ڵ�һ�������ĸ����Ƕ��٣���С����С�������Ϸ��ÿ�˸�ת������ת�̣��������������Ļ�Ϊ��������С��Ӯ���������������Ļ�Ϊ��������С��Ӯ�����Ǹ���ƽ����Ϸ����˵�����ɣ�����������״ͼ���б��ķ�����
���𰸡�![]() ������ƽ�����ɼ�����
������ƽ�����ɼ�����
��������
���ݷ��������������ʿ�֪����k��0��ͼ���ڵ�һ�������ޣ��ɴ˽�ɣ�
�������������б�������״ͼ���������еȿ��ܵij��ֽ����Ȼ����ݸ��ʹ�ʽ����������¼��ĸ��ʣ�
��2��1��0��-1��
�෴��������![]() ��ͼ���ڵ�һ�������ĸ�����
��ͼ���ڵ�һ�������ĸ�����![]() ��
��
�б��ã�
�� �� | -1 | 1 | 2 |
-1 | ��-1��-1�� | ��-1��1�� | ��-1��2�� |
1 | ��1��-1�� | ��1��1�� | ��1��2�� |
2 | ��2��-1�� | ��2��1�� | ��2��2�� |
�ɱ���֪������9�ֿ��ܵĽ����ÿ�ֽ�����ֵĿ�������ͬ�����������������Ļ�Ϊ�����Ľ����5�֣������������Ļ�Ϊ�����Ľ����4�֣�
��P��С��Ӯ��=![]() ��P��С��Ӯ��=
��P��С��Ӯ��=![]() ��
��
��С��Ӯ�ĸ��ʲ�����С��Ӯ�ĸ��ʣ�
�������Ϸ����ƽ��


 ��ʦ����ָ���ο�ʱϵ�д�
��ʦ����ָ���ο�ʱϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���֪A(1��2)��B(3��0)��������������ȡ��C��ʹ��ABCΪ���������Σ������������ĵ�C�ĸ����ǣ� ��
A.5B.6C.7D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ����
����![]() �����Բ������Բ��Բ��
�����Բ������Բ��Բ��![]() ������Ϊ__________����
������Ϊ__________����![]() ����Ϊ
����Ϊ![]() ������
������![]() ��ֱ��
��ֱ��![]() ��
��![]() ��λ�ù�ϵ��___________��
��λ�ù�ϵ��___________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ뾶Ϊ1�ġ�O��ֱ������C�ڡ�O�ϣ���CAB��30����DΪ�ӻ�CB���е㣬��P��ֱ��AB��һ�����㣬��PC+PD����СֵΪ�� ��
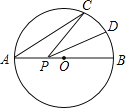
A.1B.2C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��x2+bx+c��x�ύ��A��B���㣨A��B����ࣩ����y�ύ�ڵ�C(0����3)���Գ���Ϊx��1����D��C���������ߵĶԳ���Գƣ�
��1���������ߵĽ���ʽ����D�����ꣻ
��2����P���������ϵ�һ�㣬����ABP�������8ʱ�������P�����ꣻ
��3����MΪֱ��AD�·���������һ���㣬���M�ĺ�����Ϊm����mΪ��ֵʱ����ADM�����������������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪��A��2![]() ��0����C��0����1������PΪ�߶�OA��һ���㣬��CP+
��0����C��0����1������PΪ�߶�OA��һ���㣬��CP+![]() AP����СֵΪ_____��
AP����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB��15��BC��17��������ABCD�Ƶ�D��˳ʱ�뷽����ת�õ�����DEFG����A���ھ���ABCD�ı�BC�ϣ�����CG����CG�ij���_____��
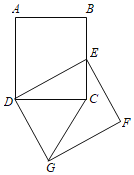
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ҫ�ڹ涨ʱ���ڰ���1200�ֻ���ԭ�ϣ�����![]() ��
��![]() ���ֻ����˿ɹ�ѡ����֪
���ֻ����˿ɹ�ѡ����֪![]() �ͻ����˱�
�ͻ����˱�![]() �ͻ�����ÿСʱ�����30���ͣ�
�ͻ�����ÿСʱ�����30���ͣ�![]() �����˰���900�����õ�ʱ����
�����˰���900�����õ�ʱ����![]() �ͻ����˰���600�����õ�ʱ����ȣ�
�ͻ����˰���600�����õ�ʱ����ȣ�
(1)�����ֻ�����ÿСʱ�ֱ���˶��ٶֻ���ԭ�ϣ�
(2)�ù���ԭ�ƻ�ͬʱʹ�������ֻ����˰��ˣ�����һ��ʱ���![]() �ͻ������������µİ����������뿪�������뱣֤��������ԭ����11Сʱ��ȫ��������ϣ���
�ͻ������������µİ����������뿪�������뱣֤��������ԭ����11Сʱ��ȫ��������ϣ���![]() �ͻ��������ٹ�������Сʱ�����ܱ�֤��������ԭ���ڹ涨��ʱ������ɣ�
�ͻ��������ٹ�������Сʱ�����ܱ�֤��������ԭ���ڹ涨��ʱ������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����۵�������С��һ��ij��ֲ�ﻨ�۵�����ԼΪ0.000037���ˣ���֪1��=1000���ˣ���ô0.000037���˿��ÿ�ѧ��������ʾΪ
A. 3.7��10��5�� B. 3.7��10��6�� C. 37��10��7�� D. 3.7��10��8��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com