
分析 (1)原式先通分,再计算减法即可求解;
(2)根据同分母分式加减法计算法则计算即可求解;
(3)原式先通分,再计算加减法即可求解;
(4)先计算同分母分式加法,再通分计算即可求解.
解答 解:(1)$\frac{2}{x-3}-\frac{6}{{x}^{2}-9}$
=$\frac{2(x+3)-6}{(x+3)(x-3)}$
=$\frac{2x}{(x+3)(x-3)}$;
(2)1+$\frac{1}{x-3}$+$\frac{1-x}{3-x}$
=$\frac{x-3+1-1+x}{x-3}$
=$\frac{2x-3}{x-3}$;
(3)$\frac{1}{x}$-$\frac{2}{3x}$+$\frac{x}{3x-2}$
=$\frac{3(3x-2)-2(3x-2)+x}{3x(3x-2)}$
=$\frac{2(2x-1)}{3x(3x-2)}$;
(4)$\frac{m}{m+n}$+$\frac{n}{m+n}$+$\frac{{m}^{2}}{{n}^{2}-{m}^{2}}$
=$\frac{m+n}{m+n}$+$\frac{{m}^{2}}{{n}^{2}-{m}^{2}}$
=1+$\frac{{m}^{2}}{{n}^{2}-{m}^{2}}$
=$\frac{{n}^{2}-{m}^{2}+{m}^{2}}{{n}^{2}-{m}^{2}}$
=$\frac{{n}^{2}}{{n}^{2}-{m}^{2}}$.
点评 考查了分式的加减法,注意分式的通分必须注意整个分子和整个分母,分母是多项式时,必须先分解因式,分子是多项式时,要把分母所乘的相同式子与这个多项式相乘,而不能只同其中某一项相乘.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
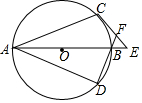 如图,AB为⊙O的直径,AC,AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为3,∠E=45°,则CF的长为6-3$\sqrt{2}$.
如图,AB为⊙O的直径,AC,AD为⊙O的弦,$\widehat{BC}$=$\widehat{BD}$,过C作⊙O的切线交AB的延长线于E,DB的延长线交CE于F,若⊙O的半径为3,∠E=45°,则CF的长为6-3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
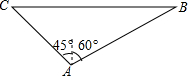 如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为(40+40$\sqrt{3}$)海里.
如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为(40+40$\sqrt{3}$)海里.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.
已知:一小球在如图所示正方形区域滚动,正方形ABCD边长为3,E、F、G、H分别为各边上的点,且AE=BF=CG=DH=1,则小球停止后正好落在阴影区域的概率是$\frac{5}{9}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com