
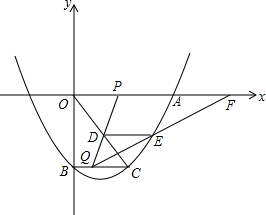
 如图,在平面直角坐标系xoy中,抛物线y=$\frac{1}{6}$x2-$\frac{4}{3}$x-8与x正半轴交于点A,与y轴交于点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P、Q分别从O、C两点同时出发,点P以每秒3个单位的速度沿OA向终点A移动,点Q以每秒2个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
如图,在平面直角坐标系xoy中,抛物线y=$\frac{1}{6}$x2-$\frac{4}{3}$x-8与x正半轴交于点A,与y轴交于点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P、Q分别从O、C两点同时出发,点P以每秒3个单位的速度沿OA向终点A移动,点Q以每秒2个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动,线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)分析 (1)令x=0求出y即可得B点坐标;将抛物线解析式写成交点式即可得出A点坐标;由于BC∥OA,所以令y=-8即可解出C点坐标;
(2)由于PA已经平行QC了,所以只需要两者相等就可以满足要求.将这两条线段用t表示,建立关于t的方程,解之即可;
(3)由于QC∥DE∥OA,则利用平行线分线段成比例可知$\frac{QC}{AF}=\frac{CE}{EA}=\frac{CD}{DO}=\frac{QC}{PO}$,从而OP=AF,则PF始终等于OA,而OA是定值;
(4)△PQF为等腰三角形,分三种情况:QP=QF;PQ=PF;FQ=FP.每种情画出相应的图形,列方程解答即可.
解答 解:(1)对于抛物线y=$\frac{1}{6}$x2-$\frac{4}{3}$x-8,令x=0,则y=-8,
∴B(0,-8),
∵y=$\frac{1}{6}$x2-$\frac{4}{3}$x-8=$\frac{1}{6}(x-12)(x+4)$,
∴A(12,0),
由于BC∥x轴,
令y=$\frac{1}{6}$x2-$\frac{4}{3}$x-8=-8,
∴x=8或x=0,
∴C(8,-8).
(2)∵PA∥CQ,
∴当PA=CQ时,PQCA为平行四边形,
∵PA=12-3t,CQ=2t,
∴12-3t=2t,
∴t=$\frac{12}{5}$,
即:当t=$\frac{12}{5}$时,PQCA为平行四边形.
(3)∵DE∥OA,
∴$\frac{CE}{EA}=\frac{CD}{DO}$,
∵QC∥OA,
∴$\frac{QC}{OP}=\frac{CD}{DO}$,$\frac{QC}{AF}=\frac{CE}{EA}$,
∴$\frac{QC}{OP}=\frac{QC}{AF}$,
∴OP=AF,
∴PF=AP+AF=AP+OP=OA=12,
即PF是定值.
(4)①若FQ=FP=12,如图1,作QM⊥x轴于点M,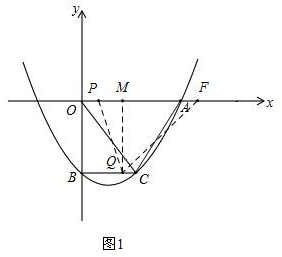
∵CQ=2t,
∴BQ=8-2t,
∵OP=3t,
∴OF=12+3t,
∴MF=OF-OM=3t+12-8+2t=4+5t,
∴QM2+MF2=QF2=144,
即:64+(4+5t)2=144,
解得t=$\frac{4\sqrt{5}-4}{5}$;
②若PF=PQ,如图2,作QH⊥x轴于点H,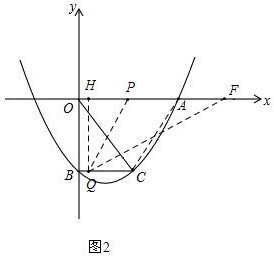
则OH=BQ=8-2t,
∴PH=3t-8+2t=5t-8,
∴PH2+HQ2=PQ2,
即:(5t-8)2+64=144,
解得t=$\frac{8+4\sqrt{5}}{5}$;
③若QP=QF,如图3,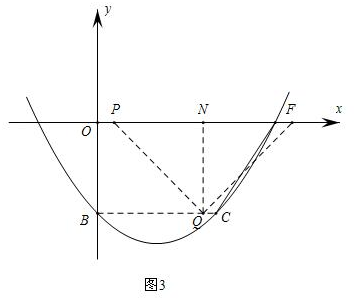
作QN⊥x轴于点N,
则PN=NF=6,且BQ=ON,
即:8-2t=6+3t,
解得t=$\frac{2}{5}$;
综上所述,当t为$\frac{2}{5}$或$\frac{4\sqrt{5}-4}{5}$或$\frac{8+4\sqrt{5}}{5}$时,△PQF为等腰三角形.
点评 本题主要考查了抛物线上特殊点的坐标求法、平行四边形的判定与性质、平行线分线段成比例、等腰三角形的性质,勾股定理等重要知识点,综合性较强,有一定难度.带速度的动点问题的基本处理思路是将相关线段用t表示,线段用t表示之后,实际上相当于将动态问题静态化了.动态问题静态处理,这是解答动态几何问题的指导思想.第(3)问是一个利用线段比例式证明两线段相等的经典例子,值得重视;第(4)问是常考的一种类型,即等腰三角形的存在性问题,其基本思路是先假定三点形成等腰三角形,然后根据等腰三角形的性质列出方程,若方程有解,就表明的确存在,若方程无解,就表明不存在.这类问题体现方程思想,同时注意这类同题往往要分类讨论,不要漏解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com