
【题目】如下图1,在四边形ABCD中,点E、F分别是AB、CD的中点.过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连结GA、GB、GC、GD、EF,若∠AGD=∠BGC.

(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:本题是相似形综合题目,考查了线段垂直平分线的性质、全等三角形的判定与性质、相似三角形的判定与性质、三角函数等知识;本题难度较大,综合性强,特别是(3)中,需要通过作辅助线综合运用(1)(2)的结论和三角函数才能得出结果.
(2)先证出∠AGB=∠DGC,由![]() =
=![]() ,证出△AGB∽△DGC,得出比例式
,证出△AGB∽△DGC,得出比例式![]() =
=![]() ,再证出∠AGD=∠EGF,即可得出△AGD∽△EGF;
,再证出∠AGD=∠EGF,即可得出△AGD∽△EGF;
(3)延长AD交GB于点M,交BC的延长线于点H,则AH⊥BH,由△AGD≌△BGC,得出∠GAD=∠GBC,再求出∠AGE=∠AHB=90°,得出∠AGE=![]() ∠AGB=45°,求出
∠AGB=45°,求出![]() =
=![]() ,由△AGD∽△EGF,即可得出
,由△AGD∽△EGF,即可得出![]() 的值即可.
的值即可.
试题解析:(1)∵GE是AB的垂直平分线,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,
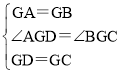 ,
,
∴△AGD≌△BGC(SAS),
∴AD=BC;
(2)∵∠AGD=∠BGC,
∴∠AGB=∠DGC,
在△AGB和△DGC中,![]() =
=![]() ,
,
∴△AGB∽△DGC,
∴![]() =
=![]() ,
,
又∵∠AGE=∠DGF,
∴∠AGD=∠EGF,
∴△AGD∽△EGF;
(3)延长AD交GB于点M,交BC的延长线于点H,如图所示,则AH⊥BH,
∵△AGD≌△BGC,
∴∠GAD=∠GBC,
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,
∴∠AGB=∠AHB=90°,
∴∠AGE=![]() ∠AGB=45°,
∠AGB=45°,
∴![]() =
=![]() ,
,
又∵△AGD∽△EGF,
∴![]() =
=![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 正比例函数是一次函数的特殊形式B. 一次函数不一定是正比例函数
C. y=kx+b是一次函数D. 2x-y=0是正比例函数
查看答案和解析>>
科目:初中数学 来源: 题型:
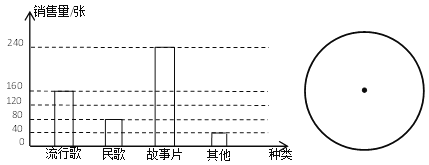
【题目】小明对某音像制品店十月份的销售量情况进行调查.如图是小明对所调查结果的条形统计图.
(1)该店十月份共销售多少张音像制品?
(2)请你改用扇形统计图来表示该店十月份销售音像制品的种类.
(3)从统计图中看,流行歌类与民歌类销售量之比是多少?故事片占总销售量的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).
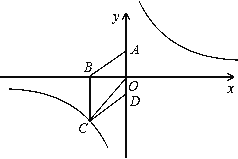
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COD的面积相等.求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在圆柱、正方体、长方体中,主视图可能一样的是 ( )
A. 仅圆柱和正方体 B. 仅圆柱和长方体
C. 仅正方体和长方体 D. 圆柱、正方体和长方体
查看答案和解析>>
科目:初中数学 来源: 题型:
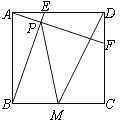
【题目】如图,正方形ABCD中,AB=4,动点E从点A出发向点D运动,同时动点F从点D出发向点C运动,点E、F运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段AF、BE相交于点P,M是线段BC上任意一点,则MD+MP的最小值为.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com