
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(-4,0).
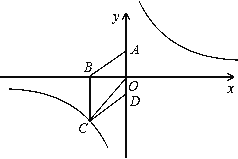
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COD的面积相等.求点P的坐标.
【答案】(1)y=![]() ;(2)P(
;(2)P(![]() ,
,![]() )或(
)或(![]() ,-
,-![]() ).
).
【解析】
试题分析:综合考查反比例函数及菱形的性质,注意:根据菱形的性质得到点C的坐标;点P的横坐标的有两种情况.
(1)根据菱形的性质可得菱形的边长,进而可得点C的坐标,代入反比例函数解析式可得所求的解析式; (2)设出点P的坐标,易得△COD的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,就求得了点P的坐标.
试题解析:(1)由题意知,OA=3,OB=4,
在Rt△AOB中,AB=![]() =5,
=5,
∵四边形ABCD为菱形,
∴AD=BC=AB=5,
∴C(-4,-5).
设经过点C的反比例函数的解析式为y=![]() (k≠0),
(k≠0),
则![]() =-5,解得k=20.
=-5,解得k=20.
故所求的反比例函数的解析式为y=![]() .
.
(2)设P(x,y),
∵AD=AB=5,OA=3,
∴OD=2,S△COD=![]() ×2×4=4,
×2×4=4,
即![]() OA|x|=4,
OA|x|=4,
∴|x|=![]() ,
,
∴x=±![]() ,、
,、
当x=![]() 时,y=
时,y=![]() =
=![]() ,当x=-
,当x=-![]() 时,y=
时,y=![]() =-
=-![]() ,
,
∴P(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2018年3月5日,十三届全国人大一次会议出席代表2970人,其中2970用科学记数法表示为( )
A. 2.97×103 B. 29.7×102 C. 0.297×104 D. 2.97×104
查看答案和解析>>
科目:初中数学 来源: 题型:
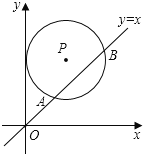
【题目】如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为![]() ,则a的值是( )
,则a的值是( )
A.2![]() B.2+
B.2+![]() C.2
C.2![]() D.2+
D.2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1)、B(x2,y2)在二次函数y=(x﹣1)2+1的图象上,若x1>x2>1,则y1_____y2(填“>”、“<”或“=”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图1,在四边形ABCD中,点E、F分别是AB、CD的中点.过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连结GA、GB、GC、GD、EF,若∠AGD=∠BGC.

(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的y与x的部分对应值如表:
X | … | 0 | 1 | 3 | 4 | … |
y | … | 2 | 4 | 2 | ﹣2 | … |
则下列判断中正确的是( )
A. 抛物线开口向上 B. y最大值为4
C. 当x>1时,y随著x的增大而减小 D. 当0<x<2时,y>2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com