
【题目】对x,y定义一种新运算T,规定:T(x,y)=ax+2by﹣1(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=a0+2b1﹣1=2b﹣1.
(1)已知T(1,﹣1)=﹣2,T(4,2)=3.
①求a,b的值;
②若关于m的不等式组 恰好有2个整数解,求实数p的取值范围;
恰好有2个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
【答案】(1)①a=1,b=3;②-2≤p<-![]() ;(2)a=2b.
;(2)a=2b.
【解析】试题分析:(1)①已知两对值代入T中计算求出a与b的值;
②根据题中新定义化简已知不等式,根据不等式组恰好有3个整数解,求出p的范围即可;
(2)由T(x,y)=T(y,x)列出关系式,整理后即可确定出a与b的关系式.
试题解析:(1)①根据题意得:T(1,-1)=![]() =-2,即a-b=-2;
=-2,即a-b=-2;
T=(4,2)=![]() =1,即2a+b=5,
=1,即2a+b=5,
解得:a=1,b=3;
②根据题意得: 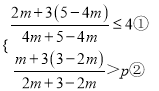 ,
,
由①得:m≥-![]() ;
;
由②得:m<![]() ,
,
∴不等式组的解集为-![]() ≤m<
≤m<![]() ,
,
∵不等式组恰好有3个整数解,即m=0,1,2,
∴2<![]() ≤3,
≤3,
解得:-2≤p<-![]() ;
;
(2)由T(x,y)=T(y,x),得到![]() =
=![]() ,
,
整理得:(x2-y2)(2b-a)=0,
∵T(x,y)=T(y,x)对任意实数x,y都成立,
∴2b-a=0,即a=2b.


科目:初中数学 来源: 题型:
【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E。

(1)求证:AB=BE;
(2)若PA=2 ,cosB=![]() ,求⊙O半径的长。
,求⊙O半径的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某县七年级9800名学生的视力情况,从中抽查了100名学生的视力情况,就这个问题来说,下面说法正确的是( )
A. 9800名学生是总体 B. 每个学生是个体
C. 100名学生是所抽取的一个样本 D. 样本容量是100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=acm,AB=bcm(a>b>4),半径为2cm的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).
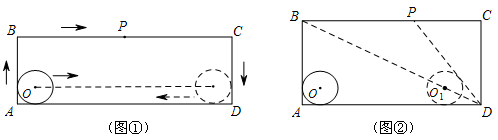
(1)如图①,点P从A→B→C→D,全程共移动了 cm(用含a、b的代数式表示);
(2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点.若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离;
(3)如图②,已知a=20,b=10.是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请求出小桥PD的长.
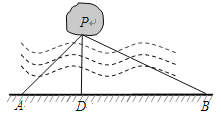
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com