
����Ŀ�����Ķ����в��ϣ��������Ӧ������
�������Բ���������˽�Բ����������2000����ǰ�����ҹ���ī�Ӹ���Բ�ĸ����һ��ͬ��Ҳ��������˼˵��Բ��һ��Բ�ģ�Բ�ĵ�Բ�ܵij�����ȣ���������ϣ����ѧ��ŷ����ø�Բ�µĶ���Ҫ��100�꣮��Բ�йصĶ����кܶ࣬���нǶ�����������֮һ��
���ǰѶ�����Բ�ϣ�һ�ߺ�Բ�ཻ����һ�ߺ�Բ���еĽǽ������нǣ�
���нǶ��������нǵĶ������������л����Ե�Բ�ܽǶ�����
���������нǶ����IJ���֤�����̣�
֤������ͼ�٣�AB���O�����ڵ�A����Բ��O����AC��ʱ�����õ���CAB��90�㣬�������нǡ�BAC�Ķ������������а�Բ���Ե�Բ�ܽǶ�����
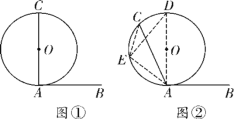
��ͼ�ڣ�AB���O�����ڵ�A����Բ��O�ڡ�BAC���ڲ�ʱ������A��ֱ��AD����O�ڵ�D����![]() ����ȡһ��E������EC��ED��EA�����CED����CAD��
����ȡһ��E������EC��ED��EA�����CED����CAD��
��
����
(1)�밴�������֤��˼·��д����֤����ʣ�ಿ�֣�
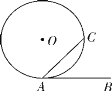
(2)��ͼ�ۣ�AB���O�����ڵ�A����Բ��O�ڡ�BAC���ⲿʱ����д�����нǶ�����֤�����̣�
���𰸡���1�������������2���������
��������
��1������Բ�ܽǶ����õ���DEA��90�����ٸ���ͬ�����Ե�Բ�ܽ���ȵõ���CED����CAD��������õ�ʽ�����ʼ��ɵõ���CEA����CAB��
��2��ͨ����C=90��˵����CFA����FAC��90�����ٸ���ͬ�ǵ������ȵõ���CAB����CFA����.
�⣺��1����AD�ǡ�Oֱ����
���DEA��90����
��AB���O�����ڵ�A��
���DAB��90����
���CED����DEA����CAD����DAB������CEA����CAB��
�����нǵĶ������������л����Ե�Բ�ܽǶ�����
��2��֤������ͼ������A��ֱ��AF����O�ڵ�F������FC��
��AF��ֱ����
���ACF��90����
���CFA����FAC��90����
��AB���O�����ڵ�A��
���FAB��90����
���CAB����FAC��90����
���CAB����CFA��
�����нǵĶ������������л����Ե�Բ�ܽǶ�����


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��10��BC��16����DΪBC���ϵ�һ�����㣨��D�����B����C�غϣ�����DΪ��������ADE����B������DE��AC���ڵ�E������A��AF��AD������DE�ڵ�F��
��1����֤��ABCE��BDCD��
��2����DFƽ�֡�ADCʱ����AE�ij���
��3������AEF�ǵ���������ʱ����BD�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��˾����ͳ����ÿ������Ա��ij�µ����۶��������������ͳ��ͼ������ͳ��ͼ��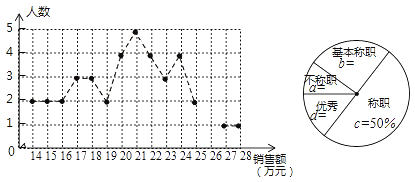
������Ա�������۶�Ϊx����λ����Ԫ�������۲��涨����x<16ʱ��Ϊ������ְ������ ![]() ʱΪ��������ְ������
ʱΪ��������ְ������![]() ʱΪ����ְ������
ʱΪ����ְ������![]() ʱΪ��������.����������Ϣ������������⣺
ʱΪ��������.����������Ϣ������������⣺
��1����ȫ����ͳ��ͼ������ͳ��ͼ��
��2������������ְ������������������Ա���۶����λ����������
��3��Ϊ�˵�������Ա�Ļ����ԣ����۲������ƶ�һ�������۶�������������۶�ﵽ�������������Ա����ý��������Ҫʹ����������ְ������������������Ա��һ����Ա�ܻ������۶����Ӧ��Ϊ������Ԫ�����ȥ��������������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ��ת�̱��ֳ�![]() �ȷ֣�ÿһ���ϸ�д��һ�����֣����ת��ת��
�ȷ֣�ÿһ���ϸ�д��һ�����֣����ת��ת��![]() �Σ���һ��ת������������Ϊʮλ���֣��ڶ���ת��������Ϊ��λ���֣�
�Σ���һ��ת������������Ϊʮλ���֣��ڶ���ת��������Ϊ��λ���֣�![]() ��ת�������һ����λ������ָ��ͣ�ڵȷ�����������תһ�Σ�
��ת�������һ����λ������ָ��ͣ�ڵȷ�����������תһ�Σ�
![]() �û���״ͼ�ķ������ת�������п��ܳ��ֵ���λ���ĸ�����
�û���״ͼ�ķ������ת�������п��ܳ��ֵ���λ���ĸ�����
![]() �ס�����������Ϸ��Լ���õ�����λ����ż��ʱ��ʤ��������ʤ�������Ϸ��ƽ����˵�����ɣ�
�ס�����������Ϸ��Լ���õ�����λ����ż��ʱ��ʤ��������ʤ�������Ϸ��ƽ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
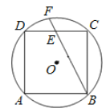
����Ŀ����ͼ��������ABCD�ڽ��ڡ�O����EΪDC���е㣬BE���ӳ��߽���O�ڵ�F������O�İ뾶Ϊ![]() ����BF�ij�Ϊ________��
����BF�ij�Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��ֱ��AM���O�Ľ��㣬��B�ڡ�O�ϣ�BD��AM������ΪD��BD���O���ڵ�C��OCƽ�֡�AOB����B��60����
��1����֤��AM�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ4����ͼ����Ӱ���ֵ������������������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��ij�ֲ�����豭��200���������ۣ����в豭�������Dz��������5������20�������۷�ʽ�����֣���1���������ۣ���2���������ۣ������Ϣ���±���
���ۣ�Ԫ/���� | �����ۼۣ�Ԫ/���� | �����ۼۣ�Ԫ/�ף� | |
��� | 24 | a | 55 |
�豭 | 4 | a��30 | |
��ע����1��һ������ͺ��ĸ��豭���һ�ף���ͼ���� ��2������=���ۼ۩����ۣ������� | |||
��1�����̵깺������Ͳ豭���ж��ٸ���
��2����֪�˿ͻ�180Ԫ����IJ���������ҹ˿ͻ�30Ԫ����IJ豭������ͬ��
�������a��ֵ��
�ڵ����̵껹ʣ��20�������100���豭ʱ���̵꽫��Щ����Ͳ豭�е�һ���ְ��������ۣ����ఴ�������ۣ���120��������豭ȫ���۳������õ�����Ϊ365Ԫ���ʳ��������˶����ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ABCD��ͼ1��ʾ����ƽ��ֱ������ϵ�У�AD����x���غϣ�����B��Cλ��x���Ϸ�����ֱ��l��y��x��3��x��������ÿ��1����λ���ȵ��ٶ�ƽ�ƣ���ƽ�ƵĹ����У���ֱ�߱�������ABCD�ı����صõ��߶γ�Ϊm��ƽ�Ƶ�ʱ��Ϊt�룬m��t�ĺ���ͼ����ͼ2��ʾ����a��b��ֵ�ֱ��ǣ�������
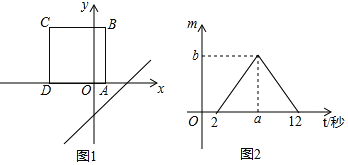
A.6��![]() B.6��
B.6��![]() C.7��7
C.7��7![]() D.7��5
D.7��5![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��OΪ![]() ����Բ��Բ�ģ���AOB��90������P��
����Բ��Բ�ģ���AOB��90������P��![]() ���˶��������A��B�غϣ���AP��OB�ӳ����ڵ�C��CD��OP�ڵ�D����OB��2BC��2����PD�ij��ǣ� ��
���˶��������A��B�غϣ���AP��OB�ӳ����ڵ�C��CD��OP�ڵ�D����OB��2BC��2����PD�ij��ǣ� ��
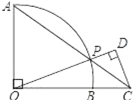
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com