
����Ŀ��![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() ������
������![]() �ϵ�һ�����㣨��
�ϵ�һ�����㣨��![]() �����
�����![]() �غϣ���
�غϣ���![]() ����
����![]() Ϊ�ߵĵȱ������Σ�����
Ϊ�ߵĵȱ������Σ�����![]() ��
��![]() ��ƽ���ߣ��ֱ�����
��ƽ���ߣ��ֱ�����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
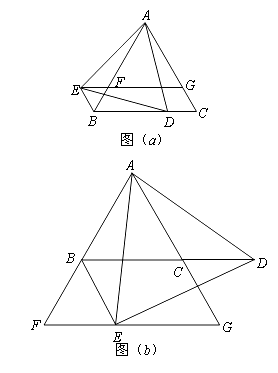
��1����ͼ��a����ʾ������![]() ���߶�
���߶�![]() ��ʱ��
��ʱ��
����֤��![]() ��
��
��̽�����ı���![]() ������������ı��Σ���˵�����ɣ�
������������ı��Σ���˵�����ɣ�
��2����ͼ��b����ʾ������![]() ��
��![]() ���ӳ�����ʱ��
���ӳ�����ʱ��
������1����������֤��̽�������������Ƿ���Ȼ��������ֱ��д��������˵�����ɣ�
������![]() �˶���ʲôλ��ʱ���ı���
�˶���ʲôλ��ʱ���ı���![]() �����Σ���˵�����ɣ�
�����Σ���˵�����ɣ�
���𰸡���1��������������ƽ���ı�����2������������BC��CD
���������⣺��1�� �� �� ��ABC����ADE���ǵȱ�������,
�� AE=AD,AB=AC,��EAD=��BAC=60��.
���� ��EAB=��EAD-��BAD,��DAC=��BAC-��BAD
�� ��EAB=��DAC,
�� ��AEB�ա�ADC�� ��������������������������������������������3�֣�
�� �ı���![]() ��ƽ���ı���. ��������������������������������6�֣�
��ƽ���ı���. ��������������������������������6�֣�
��2����1�������:
�� ��AEB�ա�ADC���� �ı���![]() ��ƽ���ı��Σ�������. ������������������8�֣�
��ƽ���ı��Σ�������. ������������������8�֣�
��3����BC��CDʱ���ı���BCFE�����Σ�������������������������������������9�֣�
���ɣ� ��������AEB�ա�ADC��
��BE��BC
���� BE��CD��
�� BC��CD��
�������ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
�� �ı���![]() �����Σ� ������������������������������������13�֣�
�����Σ� ������������������������������������13�֣�
��1����֤��������EAB����BAD����BAD����DAC��60�ȣ�������EAB����DAC����EA��DA��BA��CA������AEB�ա�ADC������������EBC����EBA����ABC����DCA����ABC��120�ȡ���ô��EBC����BCG��120�ȣ�60�ȣ�180�ȣ�����EB//GC����EG//BC����BCGEΪһƽ���ı��Ρ� ��2��BEGC��Ϊƽ���ı��Ρ��루1�����ƣ�����֤������ABEȫ���ڦ�ACD����ô��ABE����ACD��120�ȣ�������CBE����ACB��60�ȣ�����BE//GC����BC//EG���Ӷ���֤����3����ʹ���Ϊ���Σ�ֻ��BE��BC����BE��CD����ֻ��ѡȡD��ʹBC��CD���ɡ�


 ÿ�α���ϵ�д�
ÿ�α���ϵ�д� ��ѧ����ϵ�д�
��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�������B���ڵ���ǵ���140������ô��A+��C=_______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A����Ϊ(6��0)����B��y����������ϣ���![]() =240.
=240.
(1)���B���ꣻ
(2)����P��B������y�Ḻ���᷽���˶����ٶ�ÿ��2����λ���˶�ʱ��t�룬��AOP�����ΪS����S��t�Ĺ�ϵʽ����ֱ��д��t��ȡֵ��Χ��
(3)��(2)�������£���S��AOP��S��ABP=1:3����S��AOP+S��ABP=S��AOB�����߶�AB�Ĵ�ֱƽ�������Ƿ���ڵ�Q��ʹ�á�AOQ��������BPQ�������ȣ������ڣ����Q�����ꣻ�������ڣ���˵�����ɡ�



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������������ǣ�������
A.��ͬһƽ���ڣ�����ֱ�ߵ�λ��ֻ��ƽ�кʹ�ֱ����
B.��ֱ��ƽ�У�ͬ���ڽ����
C.��һ������ֻ��һ��ֱ������ֱ֪��ƽ��
D.ƽ����ͬһ��ֱ�ߵ���ֱ��ƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:��ͼ��AD��BC�ڵ�D,EG��BC�ڵ�G,��E=��3,��AD�� ��BAC��ƽ����������˵�����ɣ������������������ע���ݣ�
�⣺�ǣ��������£�

��AD��BC,EG��BC ( ��֪ ����
���4=��5=90�� ��ֱ�Ķ��壩��
��AD��_____( )��
���1=��E ( )��
��2=______(��ֱ��ƽ�У��ڴ�����ȣ���
�ߡ�E=��3����֪����
���_____=��____��������������
��ADƽ�֡�BAC�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ������������������һ���������֡��װ������ľ����ѧУ���Ѿ��ѧ���������������������˵��飮ͼ�ٱ�ʾ���Ǹ��꼶�������ռ�ܾ�������İٷֱȣ�ͼ����ѧУ��ѧ���ľ����������г������鲢�����������ݻ��Ƶ�ͳ��ͼ

��1��ѧУ�Զ�����ѧ���ľ������������˳������飿
��2�������������ݵ�ƽ��������λ�����Ƕ��٣�
��3������У���꼶����400��ѧ��������ȫУѧ������ܽ���Լ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������±��ش����⣺
x | 16 | 16.1 | 16.2 | 16.3 | 16.4 | 16.5 | 16.6 | 16.7 | 16.8 |
x2 | 256 | 259.21 | 262.44 | 265.69 | 268.96 | 272.25 | 175.56 | 278.89 | 282.24 |
��1��272.25��ƽ������������������
��2��![]() =��������������
=�������������� ![]() =��������������
=�������������� ![]() =������������
=������������
��3����![]() ����������Ϊa����4a����������
����������Ϊa����4a����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������գ�
��ͼ��ʾ����֪��1 = ��2����B = ��C�����Ƶ�AB��CD��

�������£�
�ߡ�1 = ��2����֪�����ҡ�1 = ��4��_____________________����
���2 = ��4������������.
��CE��BF��__________________________��.
���_____= ��3��________________________��
�֡ߡ�B = ��C����֪����
���3= ��B��������������
��AB��CD��_____________________________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B����ͬʱ��ԭ��O��������A��ÿ��x����λ������x��ĸ������˶�����B��ÿ��y����λ������y����������˶���
��1����|x+2y��5|+|2x��y|=0���Էֱ����1���Ӻ�A��B��������ꣻ

��2�����BAO����Ǻ͡�ABO����ǵ�ƽ�����ཻ�ڵ�P���ʣ���A��B���˶��Ĺ����У���P�Ĵ�С�Ƿ�ᷢ���仯�����������仯���������ֵ���������仯����˵����.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com