
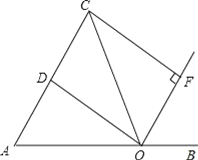
【题目】如图,点O是线段AB上的一点,OA=OC,OD平分∠AOC交AC于点D,OF平分∠COB,CF⊥OF于点F.
(1)求证:四边形CDOF是矩形;
(2)当∠AOC多少度时,四边形CDOF是正方形?并说明理由.
【答案】(1)证明见解析(2)当∠AOC=90°时,四边形CDOF是正方形,理由见解析
【解析】(1)证明:∵OD平分∠AOC,OF平分∠COB(已知),
∴∠AOC=2∠COD,∠COB=2∠COF。
∵∠AOC+∠BOC=180°,∴2∠COD+2∠COF=180°。∴∠COD+∠COF=90°。
∴∠DOF=90°。
∵OA=OC,OD平分∠AOC(已知)。
∴OD⊥AC,AD=DC(等腰三角形的“三合一”的性质)。∴∠CDO=90°。
∵CF⊥OF,∴∠CFO=90°。
∴四边形CDOF是矩形。
(2)解:当∠AOC=90°时,四边形CDOF是正方形。理由如下:
∵∠AOC=90°,AD=DC,∴OD=DC。
又由(1)知四边形CDOF是矩形,则四边形CDOF是正方形。
因此,当∠AOC=90°时,四边形CDOF是正方形。
(1)利用角平分线的性质、平角的定义可以求得∠DOF=90°;由等腰三角形的“三合一”的性质可推知OD⊥AC,即∠CDO=90°;根据已知条件“CF⊥OF”知∠CFO=90°;则三个角都是直角的四边形是矩形。
(2)当∠AOC=90°时,四边形CDOF是正方形;因为Rt△AOC的斜边上的中线OD等于斜边的一半,所以矩形的邻边OD=CD,所以矩形CDOF是正方形。


科目:初中数学 来源: 题型:
【题目】小张准备将平时的零用钱节约一些储存起来.他已存有50元,从现在起每个月节存12元.小张的同学小王以前没有存过零用钱,听到小张在存零用钱,表示从小张存款当月起每个月存18元,争取超过小张.请你写出小张和小王存款和月份之间的函数关系,并计算半年以后小王的存款是多少,能否超过小张?至少几个月后小王的存款能超过小张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,二次函数![]() 的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=
的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(3,0),OB=OC ,tan∠ACO=![]() .
.

(1)求这个二次函数的表达式;
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由;
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度;
(4)如图2,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
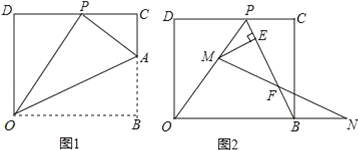
【题目】在平面直角坐标系中,O为原点,点B在x轴的正半轴上,D(0,8),将矩形OBCD折叠,使得顶点B落在CD边上的P点处.
(1)如图①,已知折痕与边BC交于点A,若OD=2CP,求点A的坐标.
(2)若图①中的点 P 恰好是CD边的中点,求∠AOB的度数.
(3)如图②,在(I)的条件下,擦去折痕AO,线段AP,连接BP,动点M在线段OP上(点M与P,O不重合),动点N在线段OB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M,N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强的钱包内有10元钱、20元钱和50元钱的纸币各1张.
(1)若从中随机取出1张纸币,求取出纸币的金额是20元的概率;
(2)若从中随机取出2张纸币,求取出纸币的总额可购买一件51元的商品的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
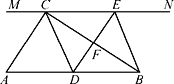
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com