
【题目】如图,D是等边三角形ABC中BA延长线上一点,连接CD,E是BC上一点,且DE=DC,若BD+BE=![]() ,CE=
,CE=![]() ,则这个等边三角形的边长是__________.
,则这个等边三角形的边长是__________.
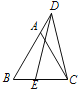
【答案】![]()
【解析】
作EK∥AC交AB于K,根据平行线的性质可得出△BEK是等边三角形,∠DKE=∠DAC,故EK=BE,再根据DE=DC可知∠DEC=∠DCE,由三角形外角的性质可知∠B+∠KDE=∠DEC,因为∠DCA+∠ACB=∠DCE,故可得出∠B+∠KDE=∠DCA+∠ACB,再由∠B=∠ACB=60°可知∠KDE=∠DCA,故可得出△EKD≌△DAC,故AD=DK,进而可得BE=AD.根据BD+BC+CE=3AB即可得出结论.
作EK∥AC交AB于K.
∵△ABC是等边三角形,∴∠B=∠ACB=∠BAC=60°,AB=BC=AC.
∵EK∥AC,∠BKE=∠BAC=60°,∠KEB=∠ACB=60°,∴△BEK是等边三角形,∠DKE=∠DAC,∴EK=BE=BK.
∵DE=DC,∴∠DEC=∠DCE,∴∠B+∠KDE=∠DCA+∠ACB.
∵∠B=∠ACB=60°,∴∠KDE=∠DCA.
在△EKD与△DAC中,∵∠DKE=∠DAC,∠KDE=∠DCA,DE=DC,∴△EKD≌△DAC(AAS),∴AD=EK,∴BE=AD.
∵BD+BE=![]() ,CE=
,CE=![]() ,∴BD+BE+2CE=
,∴BD+BE+2CE=![]() ,∴BA+AD+BC+EC=3BA=
,∴BA+AD+BC+EC=3BA=![]() ,∴AB=
,∴AB=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是 . 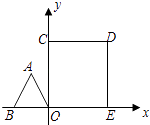
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点F在ABCD的对角线AC上,过点F,B分别作AB,AC的平行线相交于点E,连接BF,∠ABF=∠FBC+∠FCB.
(1)求证:四边形ABEF是菱形;
(2)若BE=5,AD=8,sin∠CBE= ![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了丰富学生课余活动开展了一次“爱我云南,唱我云南”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
成绩(分) | 9.40 | 9.50 | 9.60 | 9.70 | 9.80 | 9.90 |
人数 | 2 | 3 | 5 | 4 | 3 | 1 |
则入围同学决赛成绩的中位数和众数分别是( )
A.9.70,9.60
B.9.60,9.60
C.9.60,9.70
D.9.65,9.60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】昨天早晨7点,小明乘车从家出发,去西安参加中学生科技创新大赛,赛后,他当天按原路返回,如图,是小明昨天出行的过程中,他距西安的距离y(千米)与他离家的时间x(时)之间的函数图象.
根据下面图象,回答下列问题:
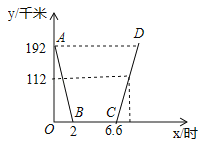
(1)求线段AB所表示的函数关系式;
(2)已知昨天下午3点时,小明距西安112千米,求他何时到家?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于点A(1,4)和点B
的图象交于点A(1,4)和点B
(![]() ,
,![]() ).
).

(1)求这两个函数的表达式;
(2)观察图象,当![]() >0时,直接写出
>0时,直接写出![]() >
>![]() 时自变量
时自变量![]() 的取值范围;
的取值范围;
(3)如果点C与点A关于![]() 轴对称,求△ABC的面积.
轴对称,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,延长
边上一点,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的垂直平分线于点
的垂直平分线于点![]() ,连接
,连接![]() .
.
(1)如图1,当点![]() 与点
与点![]() 重合时,证明:
重合时,证明:![]() ;
;

(2)如图2,当点![]() 不与
不与![]() ,
,![]() 两点重合时,(1)中的结论是否还成立?并说明理由.
两点重合时,(1)中的结论是否还成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解食品安全状况,质监部门抽查了甲、乙、丙、丁四个品牌饮料的质量,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题: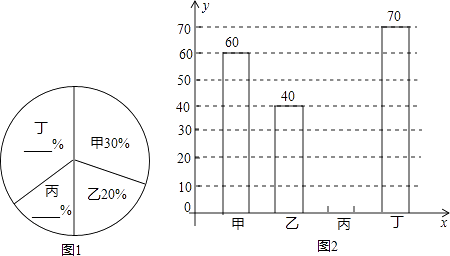
(1)这次抽查了四个品牌的饮料共瓶;
(2)请你在答题卡上补全两幅统计图;
(3)若四个品牌饮料的平均合格率是95%,四个品牌饮料月销售量约15万瓶,请你估计这四个品牌的不合格饮料有多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°

(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com