

 (2)
(2)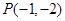 (3)
(3)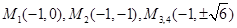
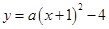 ,因为抛物线过点(0,-3),所以
,因为抛物线过点(0,-3),所以 ,解得a=1,所以抛物线的解析式
,解得a=1,所以抛物线的解析式

 ,解得x=-3,x=1,所以A点的坐标(-3,0),B点的坐标(1,0);抛物线交y轴于点C,令x=0,则
,解得x=-3,x=1,所以A点的坐标(-3,0),B点的坐标(1,0);抛物线交y轴于点C,令x=0,则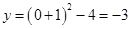 ,所以C点的坐标(0,-3);P为l上的一动点,当△PBC的周长=PB+PC+BC,因为BC的长度一定,所以要使△PBC的周长最小,即PB+PC最小,作点B关于对称轴的对称点,坐标为(-3,0),即是A点,设过A、C的直线为y=kx+b,则
,所以C点的坐标(0,-3);P为l上的一动点,当△PBC的周长=PB+PC+BC,因为BC的长度一定,所以要使△PBC的周长最小,即PB+PC最小,作点B关于对称轴的对称点,坐标为(-3,0),即是A点,设过A、C的直线为y=kx+b,则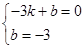
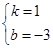 ,所以过点A、C的直线为y=x-3,则P点即为直线为y=x-3与对称轴的交点,解得
,所以过点A、C的直线为y=x-3,则P点即为直线为y=x-3与对称轴的交点,解得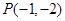
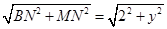 ,MC=
,MC=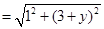 ,解得y=-1,y=
,解得y=-1,y=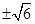 ,所以,当y=-1时M的坐标为
,所以,当y=-1时M的坐标为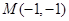 ,当y=
,当y=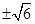 ,M的坐标为
,M的坐标为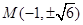 ;综上所述满足条件的M的坐标为
;综上所述满足条件的M的坐标为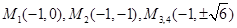


科目:初中数学 来源:不详 题型:解答题
 ,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(-2,6).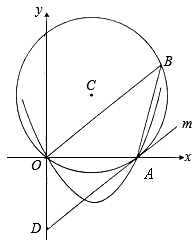
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
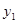 (吨)与月份
(吨)与月份 (
(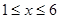 ,且
,且 取整数)之间满足的函数关系如下表:
取整数)之间满足的函数关系如下表:月份 (月) (月) | 1 | 2 | 3 | 4 | 5 | 6 |
输送的污水量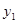 (吨) (吨) | 12000 | 6000 | 4000 | 3000 | 2400 | 2000 |
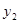 (吨)与月份
(吨)与月份 (
(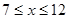 ,且
,且 取整数)之间满足二次函数关系式
取整数)之间满足二次函数关系式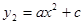 ,其图象如图所示.1至6月,污水厂处理每吨污水的费用
,其图象如图所示.1至6月,污水厂处理每吨污水的费用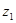 (元)与月份
(元)与月份 之间满足函数关系式
之间满足函数关系式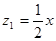 ,该企业自身处理每吨污水的费用
,该企业自身处理每吨污水的费用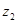 (元)与月份
(元)与月份 之间满足函数关系式
之间满足函数关系式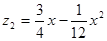 ;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.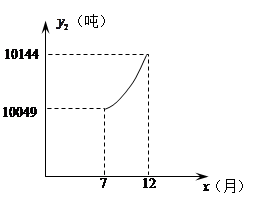
 ,
, 与
与 之间的函数关系式;
之间的函数关系式; 月用于污水处理的费用为W(元),试求出W与
月用于污水处理的费用为W(元),试求出W与 之间的函数关系式;
之间的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与y轴正半轴交于点C,连接BC、AC,CD是⊙
与y轴正半轴交于点C,连接BC、AC,CD是⊙ 的切线,AD⊥CD于点D,tan∠CAD=
的切线,AD⊥CD于点D,tan∠CAD= ,抛物线
,抛物线 过A、B、C三点.
过A、B、C三点.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
= . 
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (克)与销售时间
(克)与销售时间 (月份)之间的函数图象. (4月份以30天计算)
(月份)之间的函数图象. (4月份以30天计算)
| 商品名称 金 额 | A | B | |||
| 投资金额x(万元) | x | 5 | x | 1 | 5 |
| 销售收入y(万元) | y1=kx (k≠0) | 3 | y2=ax2+bx(a≠0) | 2.8 | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com