
 +
+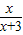 =1��
=1��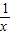 ����
����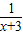 ��
�� +
+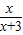 =1��
=1��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| x |
| 1 |
| x |
| 1 |
| x+3 |
| 1 |
| x+3 |
| 1 |
| x |
| 1 |
| x+3 |
| 1 |
| x+3 |
| 1 |
| x |
| 1 |
| x+3 |
| 1 |
| x+3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| x |
| 1 |
| x |
| 1 |
| x+3 |
| 1 |
| x+3 |
| 2 |
| x |
| x |
| x+3 |
| 2 |
| x |
| x |
| x+3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011����б�ҵ��ѧ���ԣ�����ʮ�߾�����ѧ ���ͣ������
����С��8�֣�ע�⣺Ϊ��ʹͬѧ�Ǹ��õؽ���⣬�����ṩ��һ�ֽ���˼·��������������˼·�������Ҫ����գ���ɱ���Ľ��Ҳ����ѡ�������Ľ��ⷽ������ʱ������գ�ֻ�谴�ս�����һ��Ҫ����н��
��һ�������ڹ涨��������ɣ�������������պ��ܹ�������ɣ�����ҵ���������Ҫ�����涨����3��. ���ڼס��Һ���2������µĹ������ҵ�����ɸպ��ڹ涨������ɣ���涨�����Ǽ��죿
���ⷽ����
��涨������Ϊx�죬
�����ú�x�Ĵ���ʽ��ʾ��
�ټĹ���Ч��Ϊ ��
���ҵĹ���Ч��Ϊ ��
���������⣬�г���Ӧ���� ��
����������̣��� ��
���������飺 ��
�������𣺹涨������ .
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com