
【题目】已知:如图,△AOB的顶点O在直线l上,且AO=AB.

(1)画出△AOB关于直线l成轴对称的图形△COD,且使点A的对称点为点C ;
(2)在(1)的条件下,AC与BD的位置关系是________;
(3)在(1)、(2)的条件下,联结AD,如果∠ABD=2∠ADB,求∠AOC的度数.
【答案】(1)作图见解析;(2)平行;(3)∠AOC=60°.
【解析】试题分析:(1)根据轴对称的性质画出图形即可;
(2)根据轴对称的性质可直接得出结论;
(3)先根据轴对称图形的性质得出△AOB≌△COD,故可得出∠OBD=∠ODB,∠ABO+∠OBD=∠CDO+∠ODB,即∠ABD=∠CDB,再由∠ABD=2∠ADB可知∠CDB=2∠ADB,故∠CDA=∠ADB,根据AC∥BD,可知∠CAD=∠ADB,∠CAD=∠CDA,所以CA=CD,故可得出AO=OC=AC,即△AOC为等边三角形.
试题解析:(1)如图1所示;
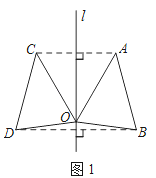
(2)∵AC与BD是对应点的连线,
∴AC∥BD,
故答案为:平行;
(3)如图2,∵由(1)可知,△AOB与△COD关于直线l对称,
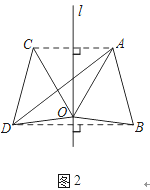
∴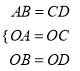 ,
,
∴△AOB≌△COD,
∴∠OBD=∠ODB,
∴∠ABO+∠OBD=∠CDO+∠ODB,即∠ABD=∠CDB,
∵∠ABD=2∠ADB,
∴∠CDB=2∠ADB,
∴∠CDA=∠ADB,
由(2)可知,AC∥BD,∴∠CAD=∠ADB.∴∠CAD=∠CDA,
∴CA=CD,
∵AO=AB,
∴AO=OC=AC,即△AOC为等边三角形,
∴∠AOC=60°.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
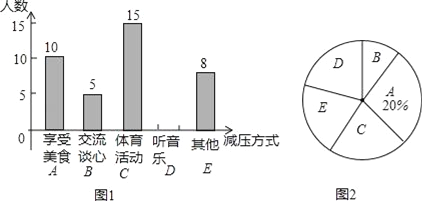
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=![]() ﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )
﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
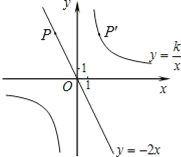
【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求a的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAC=60°,AC与BC交于点O,E为CD延长线上的一点,且CD=DE,连接BE分别交AC、AD于点F、G,连接OG,则下列结论中一定成立的是 . (把所有正确结论的序号都填在横线上) ①OG= ![]() AB;
AB;
②与△EGD全等的三角形共有5个;
③S四边形CDGF>S△ABF;
④由点A、B、D、E构成的四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
(1)求证:△ADC≌△ECD;
(2)当点D在什么位置时,四边形ADCE是矩形,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com