
【题目】三角形中有3个角、3条边共6个元素,由其中的已知元素,求出所有未知元素的过程,叫做解三角形.
已知△ABC中,AB=![]() ,∠B=45°,BC=1+
,∠B=45°,BC=1+![]() ,解△ABC.
,解△ABC.
 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
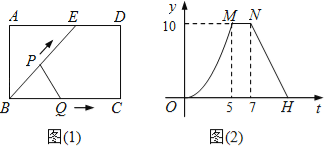
【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②cos∠ABE=![]() ;③当0<t≤5时,y=
;③当0<t≤5时,y=![]() t2;④当t=
t2;④当t=![]() 秒时,△ABE∽△QBP;其中正确的结论是 (填序号).
秒时,△ABE∽△QBP;其中正确的结论是 (填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
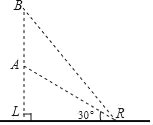
【题目】如图所示,运载火箭从地面L处垂直向上发射,当火箭到达A点时,从位于地面R处的雷达测得AR的距离是40km,仰角是30°,n秒后,火箭到达B点,此时仰角是45°,则火箭在这n秒中上升的高度是_____km.
查看答案和解析>>
科目:初中数学 来源: 题型:
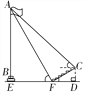
【题目】金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高.如图1-3-32,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°.已知升旗台的高度BE为1 m,点C距地面的高度CD为3 m,台阶的坡角为30°,且点E,F,D在同一直线上,求旗杆AB的高.(计算结果精确到0.1 m,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,OC边在x轴上点A、D、C共线,反比例函数y=![]() 在第一象限的图象经过点B,则△OAC和△BAD的面积之差为_____(用含k的代数式表示).
在第一象限的图象经过点B,则△OAC和△BAD的面积之差为_____(用含k的代数式表示).
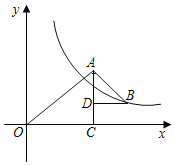
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[问题背景]![]() 三边的长分别为
三边的长分别为![]() ,求这个三角形的面积.
,求这个三角形的面积.
小辉同学在解这道题时,先建立一个正方形网格(每个小正方形的边长为![]() ),再在网格中作出格点
),再在网格中作出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),如图1所示,这样不需要作
三个顶点都在小正方形的顶点处),如图1所示,这样不需要作![]() 的高,借用网格就能计算出
的高,借用网格就能计算出![]() 的面积为_ ;
的面积为_ ;
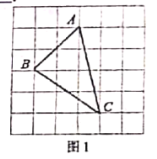
[思维拓展]我们把上述求![]() 面积的方法叫做构图法,若
面积的方法叫做构图法,若![]() 三边的长分别为
三边的长分别为![]() ,请利用图2的正方形网格(每个小正方形的边长为
,请利用图2的正方形网格(每个小正方形的边长为![]() )画出相应的
)画出相应的![]() ,并求出它的面积:
,并求出它的面积:
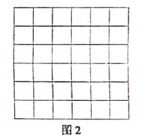
[探索创新]若![]() 三边的长分别为
三边的长分别为![]() (其中
(其中![]() 且
且![]() ),请利用构图法求出这个三角形的面积(画出图形并计算面积).
),请利用构图法求出这个三角形的面积(画出图形并计算面积).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com