
【题目】如图,已知函数y=![]() (x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E
(1)若AC=![]() OD,求a、b的值;
OD,求a、b的值;
(2)若BC∥AE,求BC的长.

【答案】(1)![]() ,
, ![]() (2)
(2)![]()
【解析】试题分析:(1)首先利用反比例函数图象上点的坐标性质得出k的值,再得出A、D点坐标,进而求出a,b的值;
(2)设A点的坐标为:(m, ![]() ),则C点的坐标为:(m,0),得出tan∠ADF=
),则C点的坐标为:(m,0),得出tan∠ADF= ,tan∠AEC=
,tan∠AEC= ,进而求出m的值,即可得出答案.
,进而求出m的值,即可得出答案.
试题解析:(1)∵点B(2,2)在函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=4,则y=![]() ,
,
∵BD⊥y轴,∴D点的坐标为:(0,2),OD=2,
∵AC⊥x轴,AC=![]() OD,∴AC=3,即A点的纵坐标为:3,
OD,∴AC=3,即A点的纵坐标为:3,
∵点A在y=![]() 的图象上,∴A点的坐标为:(
的图象上,∴A点的坐标为:(![]() ,3),
,3),
∵一次函数y=ax+b的图象经过点A、D,
∴ ,
,
解得: ![]() ,b=2;
,b=2;
(2)设A点的坐标为:(m, ![]() ),则C点的坐标为:(m,0),
),则C点的坐标为:(m,0),
∵BD∥CE,且BC∥DE,
∴四边形BCED为平行四边形,
∴CE=BD=2,
∵BD∥CE,∴∠ADF=∠AEC,
∴在Rt△AFD中,tan∠ADF= ,
,
在Rt△ACE中,tan∠AEC= ,
,
∴![]() =
=![]() ,
,
解得:m=1,
∴C点的坐标为:(1,0),则BC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知AB⊥BC,DC⊥BC,∠1=∠2,可得到BE∥CF,说明过程如下,请填上说明的依据:
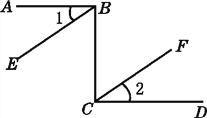
因为AB⊥BC,DC⊥BC,
所以∠ABC=90°,
∠BCD=90°(______________),
所以∠ABC=∠BCD.
又因为∠1=∠2,
所以∠EBC=∠FCB.
所以BE∥CF(______________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句是命题的个数( )
(1)延长线段AB,(2)两条直线相交,只有一交点,(3)画线段AB的中点,(4)若|x|=2,则x=2,(5)角平分线是一条射线.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张长方形纸片ABCD按图中的方式折叠,使点A与点E重合,点C与点F重合(E,F两点均在BD上),折痕分别为BH,DG.试说明:△BHE≌△DGF.
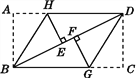
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△POQ中,OP=OQ=4,M是PQ中点,∠P=∠Q=45°,将一三角尺的直角顶点放在点M处,以M为旋转中心旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.试说明:MA=MB.
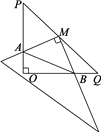 +
+
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.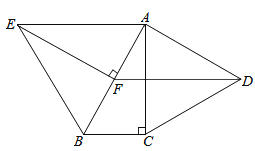
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com