
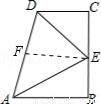
在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,如图,则下列说法正确的有几个,大家一起热烈地讨论交流,小红第一个得出正确答案,是( ).

(1)AE平分∠DAB;
(2)△EBA≌△DCE;
 (3)AB+CD=AD;
(3)AB+CD=AD;
(4)AE⊥DE.(5)AB//CD
(A)2个 (B)3个 (C)4个 (D)5个
C
【解析】
试题分析:取AD的中点F,连接EF.
∵∠B=∠C=90°,
∴AB∥CD;
∵E是BC的中点,F是AD的中点,
∴EF∥AB∥CD,2EF=AB+CD
∴∠CDE=∠DEF
∵DE平分∠ADC,
∴∠CDE=∠FDE=∠DEF,
∴DF=EF;
∵F是AD的中点,∴DF=AF,
∴AF=DF=EF,
∴AF+DF=AB+CD,即AD=AB+CD;
∴∠FAE=∠FEA,
由AB∥EF可得∠EAB=∠FEA,
∴∠FAE=∠EAB,即EA平分∠DAB;
由结论(1)和DE平分∠ADC,且DC∥AB,可得∠EDA+∠DAE=90°,则∠DEA=90°,即AE⊥DE;
由以上结论及三角形全等的判定方法,无法证明△EBA≌△DCE.
正确的结论有4个,故选C.
考点: 1.三角形的全等;2.平行线的性质


科目:初中数学 来源:2014-2015学年江苏省附中八年级上学期期中考试数学试卷(解析版) 题型:选择题
下列四组线段中,可以构成直角三角形的是( )
A.4,5,6 B.1.5,2, 2.5 C.2,3,4 D.1, , 3
, 3
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省靖江市共同体九年级上学期期中考试数学试卷(解析版) 题型:解答题
(本题12分)已知关于 的方程
的方程 .
.
(1)求证:无论 取什么实数值,这个方程总有实数根;
取什么实数值,这个方程总有实数根;
(2)能否找到一个实数 ,使方程的两实数根互为相反数?若能找到,求出
,使方程的两实数根互为相反数?若能找到,求出 的值;若不能,请说明理由.
的值;若不能,请说明理由.
(3)当等腰三角形ABC的边长 ,另两边的长
,另两边的长 恰好是这个方程的两根时,求△ABC的周长.
恰好是这个方程的两根时,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省上学期九年级第一次段考数学试卷(解析版) 题型:解答题
(8分)如图所示在平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE=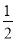 CD.
CD.
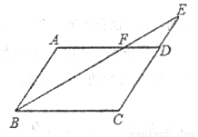
(1)求证:△ABF∽△CEB;
(2)若S△DEF面积为2,求S平行四边形ABCD的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com