
【题目】如图,四边形![]() 是一张放在平面直角坐标系中的长方形纸片,
是一张放在平面直角坐标系中的长方形纸片,![]() 为原点,点
为原点,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() .在
.在![]() 边上取一点
边上取一点![]() ,将纸片沿
,将纸片沿![]() 翻折,使点
翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处.
处.
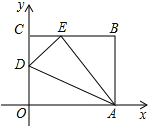
(1)求![]() 和
和![]() 的长;
的长;
(2)求直线![]() 的表达式;
的表达式;
(3)直线![]() 与
与![]() 平行,当它与矩形
平行,当它与矩形![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
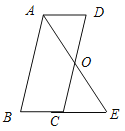
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,矩形OABC的边OA、OC分别落在x轴、y轴上,O为坐标原点,且OA=8,OC=4,连接AC,将矩形OABC对折,使点A与点C重合,折痕ED与BC交于点D,交OA于点E,连接AD,如图①. 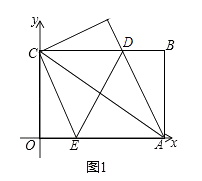
(1)求点D的坐标和AD所在直线的函数关系式;
(2)⊙M的圆心M始终在直线AC上(点A除外),且⊙M始终与x轴相切,如图②. 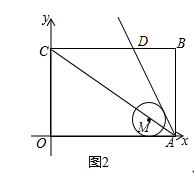
①求证:⊙M与直线AD相切;
②圆心M在直线AC上运动,在运动过程中,能否与y轴也相切?如果能相切,求出此时⊙M与x轴、y轴和直线AD都相切时的圆心M的坐标;如果不能相切,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】县内某小区正在紧张建设中,现有大量的沙石需要运输,“建安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“建安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“建安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米;
②出发1小时,货车与小汽车相遇;
③小汽车的速度是货车速度的2倍;
④出发1.5小时,小汽车比货车多行驶了60千米.

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:∠1和∠4是AB、_______被_______所截得的________角,∠3和∠5是_______、_____被_______所截得的_________角,∠2和∠5是______、_______被_______所截得的________角,AC、BC被AB所截得的同旁内角是________.
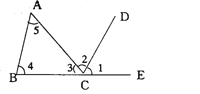
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OE⊥AB于O,若∠BOD=40°,则不正确的结论是( )

A.∠AOC=40° B.∠COE=130° C.∠EOD=40° D.∠BOE=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小米手机越来越受到大众的喜爱,各种款式相继投放市场,某店经营的A款手机去年销售总额为50000元,今年每部销售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少20%.
(1)今年A款手机每部售价多少元?
(2)该店计划新进一批A款手机和B款手机共60部,且B款手机的进货数量不超过A款手机数量的两倍,应如何进货才能使这批手机获利最多?
A,B两款手机的进货和销售价格如下表:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“数学魔盗团”社团准备购买A,B两种魔方,已知购买2个A种魔方和6个B种魔方共需130元,购买1个A种魔方比1个B种魔方多花5元.

(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买A,B两种魔方共100个(其中A种魔方不超过50个).“双11期间”某商店有两种优惠活动,如图所示.请根据以上信息填空:购买A种魔方________个时选择活动一盒活动二购买所需费用相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com