
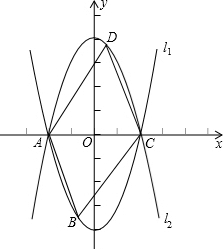
 如图,抛物线l1:y=x2-4的图象与x轴交于A,C两点,抛物线l2与l1关于x轴对称.
如图,抛物线l1:y=x2-4的图象与x轴交于A,C两点,抛物线l2与l1关于x轴对称.分析 (1)根据抛物线l1的解析式求出点A、C的坐标,以及顶点坐标,再根据关于x轴对称的点的横坐标不变,纵坐标互为相反数,求出l2的顶点坐标,然后利用待定系数法求出l2的解析式;
(2)设点B的坐标为(x1,x12-4),根据平行四边形的性质和关于原点对称的点的横坐标与纵坐标都互为相反数求出点D的坐标,代入解析式即可证明:点D在l2上;
(3)首先表示出S的值,当点B在x轴下方时,-4≤y1<0,根据一次函数的增减性判断出点B的位置,再根据对角线互相垂直平分的四边形是菱形证明,并求出S最大=16.
解答 解:(1)∵l1与x轴的交点A(-2,0),C(2,0),顶点坐标是(0,-4),l1与l2关于x轴对称,
∴l2过A(-2,0),C(2,0),顶点坐标是(0,4),
设y=ax2+4,
则4a+4=0,
解得a=-1,
∴l2的解析式为y=-x2+4;
(2)设B(x1,y1),
∵点B在l1上,
∴B(x1,x12-4),
∵四边形ABCD是平行四边形,A、C关于O对称,
∴B、D关于O对称,
∴D(-x1,-x12+4),
将D(-x1,-x12+4)的坐标代入l2:y=-x2+4,
∴左边=右边,
∴点D在l2上;
(3)当y=0时,-x2+4=0,
解得:x1=2,x2=-2,
所以AC=4,
则S?ABCD=AC•(-yB)=-4x2+16,
当x=0时,S?ABCD取得最大值16,
∵当点B在x轴下方时,-4≤y1<0,
∴S=-4y1,它是关于y1的正比例函数且S随y1的增大而减小,
∴当y1=-4时,S有最大值16,但它没有最小值,
此时B(0,-4)在y轴上,它的对称点D也在y轴上,
∴AC⊥BD,
∴平行四边形ABCD是菱形.
点评 本题是二次函数综合题型,主要利用了关于x轴对称的点的坐标,待定系数法求二次函数解析式,二次函数图象上点的坐标特征,平行四边形的性质和菱形的判定,利用一次函数的增减性求最值问题.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:解答题
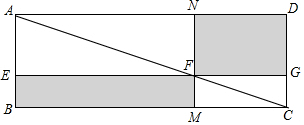 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.
数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com